Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 17

Pequenas partículas esféricas, com diâmetro D   =   50   μ m , contém um material fluorescente que, quando irradiado com luz branca, emite em um comprimento de onda correspondente à temperatura do material. Assim, a cor das partículas varia com a temperatura. Estando as pequenas partículas suspensas em água líquida, um pesquisador deseja usá-las para medir

temperaturas instantâneas locais da água em escoamentos turbulentos através da observação da cor emitida. Sendo as partículas caracterizadas por uma massa específica, um calor específico e uma condutividade térmica de ρ   =   999   k g / m 3 ,   c p   =   1200   J / ( k g   ·   K ) , e k   =   1,2   W / ( m   ·   K ) , respectivamente, determine a constante de tempo das partículas. Sugestão: Como as partículas viajam com o escoamento, a transferência de calor entre as partículas e o fluido ocorre por condução. Suponha comportamento de capacitância global.

Passo 1

Vamos lá! Nosso problema nos pede a constante de tempo térmica, mas antes que tal desenharmos um esboço do comportamento desse problema pra entendermos o que o ocorre. Fica assim.

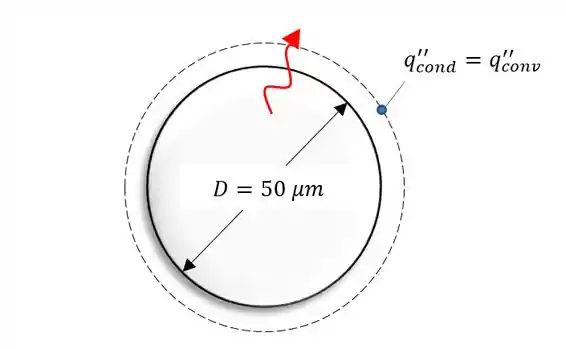
Agora vamos as nossas famosas considerações pra resolver nosso problema.

I - P r o p r i e d a d e s   c o n s t a n t e s

I I - M e i o   i n f i n i t o  

I I I - C o m p o r t a m e n t o   d e   c a p a c i t â n c i a   g l o b a l

Passo 2

Agora vamos calcular a constante de tempo térmica, mas antes como estamos tratando a troca de calor entre a partícula e a água como condução, vamos precisar do auxílio tabela 4.1 e considerarmos como o caso 1 com z → ∞ , assim o fator de forma fica:

S = 2 π D

Assim a troca de calor entre as superfícies é dada por:

q = S k T - T ∞ = h A T - T ∞ = h π D 2 T - T ∞

h = 2 k D

Passo 3

Agora finalmente podemos calcular a nossa constante de tempo térmica ( * _ _ * ) , usando a equação 5.7 temos

τ t = ρ V c h A s

Lembrando que V A s = D 6 e substituindo tudo temos:

τ t = ρ c D 6 2 k D

τ t = ρ c D 2 12 k

Por fim:

τ t = 999   k g m 3 ⋅ 1200   J k g ⋅ K ⋅ 50 ⋅ 10 - 6   m 2 6 ⋅ 0,613   W m ⋅ K = 4,07 ⋅ 10 - 8   s

τ t = 4,07 ⋅ 10 - 8   s e g u n d o s

Isso é tudo pessoal!

Resposta

τ t = 4,07 ⋅ 10 - 8   s e g u n d o s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pessoa é encontrada morta às 5h da tarde em uma sala cuja temperatura é de 20 ℃ ℃. A temperatura do corpo quando encontrado foi medida a 25 ℃ ℃, e o coeficiente de transferência de calor foi estim
Um estudante calcula que a transferência total de calor de uma bola esférica de cobre de 18c m de diâmetro inicialmente a 200 ℃ ℃ em uma ambiente a uma temperatura constante de 25 ℃ ℃, durante os prim
Na unidade de processamento de carne, bifes k = 0,45W / m ⋅ Keα = 0,91 × 10 - 7m 2 / s de 2c m de espessura, que estão inicialmente a 25 ℃ ℃, devem ser resfriados pela passagem em uma câmara frigorífi
Para fins de transferência de calor, um ovo pode ser considerado uma esfera de 6c m de diâmetro com propriedades da água. Um ovo que está inicialmente a 8 ℃ ℃ é jogado na água fervendo a 100 ℃ ℃. O co
Um eixo cilíndrico longo de aço inoxidável 304 k = 14,9W / m ⋅ K ,ρ = 7.900k g / m 3 ,c p = 477J / k g ⋅ Keα = 3,95 × 10 - 6m 2 / s de 35c m de diâmetro deixa uma estufa a uma temperatura uniforme de