Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 12

Sistemas de armazenamento de energia térmica normalmente envolvem um leito de esferas sólidas, através do qual um gás quente escoa se o sistema estiver sendo carregado ou um gás frio se o sistema estiver sendo descarregado. Em um processo de carregamento, a transferência de calor do gás quente aumenta a energia térmica armazenada nas esferas mais frias; durante a descarga, a energia armazenada diminui na medida em que calor é transferido das esferas quentes para o gás mais frio.

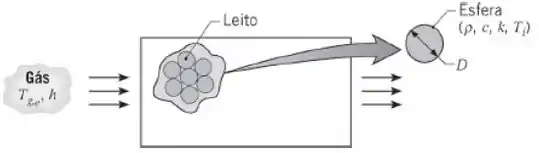
Considere um leito de esferas de alumínio ( ρ   =   2700 k g m 3 ,   c   =   950 J k g · K ,   k   =   240 W m   ·   K ) com 75   m m de diâmetro e um processo de carregamento no qual o gás entra na unidade de armazenamento a uma temperatura T g , e   =   300 ° C . Sendo a temperatura inicial das esferas T i   = 25 ° C e o coeficiente de transferência de calor h   =   75 W m 2 · K , quanto tempo demora para uma esfera próximo à entrada do sistema acumular 90 % da energia térmica máxima possível? Qual é a temperatura correspondente no centro da esfera? Há alguma vantagem em se usar cobre no lugar do alumínio?

Passo 1

Vamos lá! Nosso problema nos pede o tempo necessário para as esferas de alumínio atingirem 90% da energia térmica máxima possível e a temperatura no centro da esfera pra esse momento, mas antes que tal desenharmos o comportamento desse problema pra entendermos o que o ocorre. Fica assim.

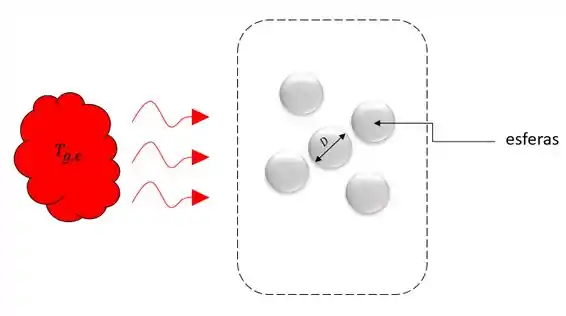
Agora vamos as nossas famosas considerações pra resolver nosso problema.

I - P r o p r i e d a d e s   c o n s t a n t e s

I I - T r o c a   d e   c a l o r   e n t r e   a s   e s f e r a s   p o r   r a d i a ç ã o   o u   c o n d u ç ã o   d e p r e z í v e l  

Passo 2

Agora vamos calcular o número de B i o t pra verificar nossa condição de troca de calor desprezível, lembrando que L c = D 6 . Calculando nosso número de B i o t temos:

B i = h L c k = 75 W m 2 ⋅ K ⋅ 75 ⋅ 10 - 3 m 6 ⋅ 240   W m ⋅ K = 0,004

Como B i ≪ 0,1 a consideração que transferência de calor entre as esferas é desprezível, se torna aceitável!

Passo 3

Agora para encontrarmos o tempo necessário pra chegarmos à temperatura que é solicitada vamos aplicar nossa equação 5.08 a , assim temos:

Q = ρ V c θ i 1 - e - t τ t

Como Q é a variação de energia interna e ρ V c θ i são os parâmetros do solido temos que Q / ρ V c θ i será a energia térmica percentual do corpo durante o processo, assim temos:

Como queremos o tempo pra chegarmos até 90 % da capacidade máxima.

Q ρ V c θ i = 0,9 = 1 - e - t τ t   I

Sendo τ t = ρ V c h A s e V A s = D 6 , temos.

τ t = ρ V c h A s = 2700   k g m 3 ⋅ 0,075   m ⋅ 950   J k g ⋅ K 6 ⋅ 75   W m 2 ⋅ K = 427,5   s

Substituindo na equação I .

0,9 = 1 - e - t 427,5

e - t 427,5 = 0,1

Aplicando o l n pra temos:

- t 427,5 = ln ⁡ 0,1 ,   t = 984   s

t = 16   m i n u t o s   e   24   s e g u n d o s

Passo 4

Agora para encontramos a temperatura no centro da esfera vamos usar a equação 5.6 , que nos dá a temperatura em qualquer lugar da esfera, assim temos:

T t = T g , e + T i - T g , e ⋅ e - t τ t

T 984 = 300 ° C - 275 ° C ⋅ e - 984 427,5

T 984 = 272,5   ° C

Passo 5

Se formos na tabela A - 1 e procurarmos pelos dados do cobre, vamos encontrar:

ρ c = 8900 k g m 3 ,   c c = 400 J k g ⋅ K

ρ c ⋅ c c = 3,56 ⋅ 10 6 J m 3 ⋅ K

Se fizermos o mesmo pro alumínio, temos:

ρ a l = 200 k g m 3 ,   c a l = 950 J k g ⋅ K

ρ a l ⋅ c a l = 2,565 ⋅ 10 6 J m 3 ⋅ K

Se compararmos os dois temos que

ρ c ⋅ c c ρ a l ⋅ c a l = 1,388

Como são propriedades diretamente ligadas a capacidade térmica se tornarmos isso em porcentagem temos

1,388 ⋅ 100 % = 138,8 %

Logo o cobre é capaz de armazenar 38,8 % mais energia térmica que o alumínio, assim para os mesmos instantes as propriedades térmicas seriam maiores.

Isso é tudo pessoal!

Resposta

t = 16   m i n u t o s   e   24   s e g u n d o s

T 984 = 272,5   ° C

Um aumento de 38,8 % na energia térmica.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa de bronze quente está tendo a superfície superior refrigerada por jato de ar a uma temperatura de 15 ℃ ℃, e o coeficiente de transferência de calor por convecção é de 220W / m 2 ⋅ K . A plac
Um ovo comum pode ser tratado como uma esfera de 5,5c m de diâmetro cujas propriedades são aproximadamente k = 0,6W / m ⋅ K e α = 0,14 × 10 - 6m 2 / s . O ovo está inicialmente a uma temperatura unifo
Considere uma casca de satélite esférica com diâmetro externo de 4m e espessura de casca de 10m m reentrando na atmosfera. A casca do satélite é feita de aço inoxidável com propriedades de ρ = 8239k g
Uma experiência deve ser conduzida para determinar o coeficiente de transferência de calor na superfície de tomates colocados em água fria a 7 ℃ ℃. Os tomates ( k = 0,59W / m ⋅ K ,α = 0,141 × 10 - 6m
No processo de recozimento, uma placa de aço inoxidável de 50m m de espessura ( ρ = 8.238k g / m 3 ,c p = 468J / k g ⋅ K,k = 13,4W / m ⋅ Keα = 3,48 × 10 - 6m 2 / s ) foi reaquecida no forno a uma temp