Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 109
Uma tigela é invertida e emborcada em um fluido denso, com densidade relativa . A tigela é mantida a uma profundidade de medida ao longo de sua linha central e a partir do seu fundo externo. A tigela tem uma altura de e o fluido denso penetra dentro dela. A tigela é única: o diâmetro interno da base vale , e ela é feita de uma velha receita de barro, de densidade relativa . O volume da tigela é aproximadamente . Qual é a força necessária para mantêla no local?
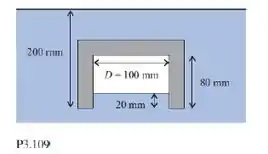
Passo 1
Nessa questão temos um tigela invertida e fluido denso. Devemos encontrar a força para manter a mesma no lugar. Para isso, suponhamos um fluido é estático e incompressível, utilizando as seguintes equações:
, força de empuxo
, somatório de forças no sentido de
Passo 2
Pelo diagrama podemos fazer a seguinte analise de forças:
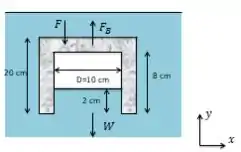
Calculando a força:
Para a força flutuante, temos:
Para o peso, temos:
Consequentemente, substituindo na nossa primeira expressão:
Prontinho!!