Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 51
Pinos (aletas) devem ser especificados para o uso em uma aplicação industrial de resfriamento. As aletas serão submetidas a um gás em escoamento cruzado com V = 10 m/s. Os pinos cilíndricos têm um diâmetro de D = 15 mm e a área da seção transversal é a mesma para cada uma das configurações mostradas no esboço.
Para pinos de igual comprimento e, consequentemente, de igual massa, qual pino (configuração) terá a maior taxa de transferência de calor? Suponha que as propriedades do gás são iguais as da água a T = 350 K. Sugestão: Suponha que os pinos possam ser tratados como infinitamente longos e use a correlação de Hilpert para o pino de seção transversal circular.
Passo 1
A primeira coisa que vamos fazer nesse exercício é pegar a propriedade do gás na temperatura de 350 K, então, como o enunciado nos disse que suas propriedades são iguais as da água a 350 K, no entanto, fazendo isso, não chegamos em valores plausíveis mais pra frente, o correto é utilizar a aproximação para o ar a essa temperatura, e nesse caso teremos:
Beleza! O enunciado nos disse que podemos considerar uma aleta com comprimento infinito, dessa forma, a taxa de transferência de calor será dada por:
Agora, sabemos que o coeficiente convectivo se relaciona com o número de Nusselt pela seguinte equação:
E para esse exercício iremos utilizar a correlação de Hilpert, que é dada por:
Então, vamos substituir a relação para na equação do calor e depois substiutir a relação para Nusselt, chegando em:
Passo 2
Então, podemos ver que os termos que vão variar de acordo com a configuração serão e , os outros serão constantes com relação as geometrias, então, podemos analisar somente o termo:
Quanto maior for esse termo, maior será o valor do calor a ser transferido. Então precisamos analisar esses valores para todas as geometrias. Precisamos dos valores das constantes e . Para a geometria circular, os valores são encontrados através da tabela 7.2 apresentada a seguir:
E, para as demais geometrias, os valores são dados pela tabela 7.3:
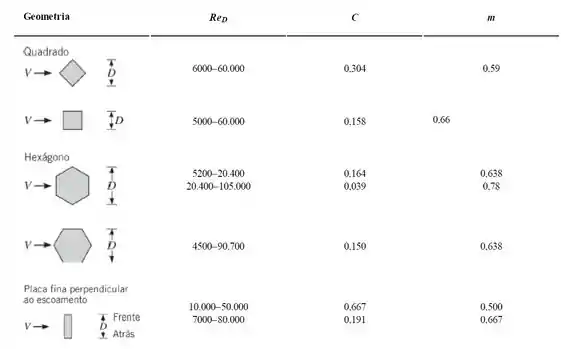
Então precisaremos calcular o número de Reynolds para os escoamentos para encontrar o valor das constantes.
Passo 3
Começando pela configuração A, temos:
Para esse número de Reynolds, teremos:
Agora, precisamos do perímetro , que será dado por:
Então a relação que estamos analisando será:
Passo 4
Beleza, agora precisamos repetir o processo para a configuração B, calculando o número de Reynolds com o D equivalente, que será o lado do quadrado. Nesse caso, como o enunciado nos disse que a área transversal das configurações seria a mesma, então, sabendo que a área do quadrado é dada pela multiplicação do comprimento do seu lado, teremos um equivalente de:
Então, calculando Reynolds com esse valor, temos:
Para esse número de Reynolds, teremos:
Agora, precisamos do perímetro , que será dado por:
Então, substituindo os valores conhecidos na relação de interesse, temos:
Passo 5
Agora iremos para a configuração C, de acordo com a tabela do passo 2, o diâmetro equivalente D é a altura do diamante, ou seja, a diagonal do quadrado, que é dada por:
O lado o quadrado já foi encontrado no passo 4, então teremos:
Então, calculando Reynolds com esse valor, temos:
Para esse número de Reynolds, teremos:
Agora, precisamos do perímetro , que será dado por:
Então, substituindo os valores conhecidos na relação de interesse, temos:
Então, comparando os três valores, podemos ver que a configuração B é aquela que vai fornecer a maior taxa de transferência de calor.