Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 7.Problemas - Ex. 38
38 – Determine o coeficiente de transferência de calor por convecção, a resistência térmica para a convecção, e a taxa de transferência de calor por convecção que são associados com ar na pressão atmosférica em um fluxo cruzado sobre um cilindro de diâmetro D=100 mm e comprimento L=2 m. A temperatura do cilindro é TS=70°C enquanto que a velocidade e a temperatura do ar são V=3 m/s e , respectivamente. Plote o coeficiente e a taxa de transferência de calor por convecção do cilindro para uma faixa de 0,05 m ≤ D ≤ 0,5 m.
Passo 1
Nesta questão, você basicamente vai trabalhar com expressões que você estudou e viu no capítulo 7 do Incropera. Para determinar o coeficiente de transferência de calor por convecção você pode usar a relação de Nusselt. Já para a resistência térmica você aplicar a definição de resistência térmica que é definido como a força motriz da transferência de calor, que é a variação de temperatura ΔT, pela quantidade de calor transferido, q. E por final com a resistência térmica encontrada você consegue achar o valor da transferência de calor por convecção.
Passo 2
Vamos começar com Nusselt, Nu, cuja expressão é
Onde,
-h é o coeficiente de transferência de calor por convecção;
-D é o diâmetro do cilindro;
-k é a condutividade térmica do fluido.
Isolando h
Para determinarmos o valor de Nu, você pode lembrar que existem várias correlações empíricas o seu cálculo. Mas, você deve atentar que não é qualquer correlação empírica que é aplicada para este caso que se trata de fluxo cruzado em um cilindro. Assim temos que pegar uma correlação apropriada para este caso.
Uma correlação aplicada para fluxo cruzado em cilindros é a correlação de Hilpert que é mais prática e simples do que outras, então vamos usa-la. A correlão de Hilpert é a seguinte:
Onde,
-C e m são constantes encontradas em tabelas;
-Re e Pr são o número de Reynolds e número de Prandtl, respectivamente.
Então, para acharmos h:
Passo 3
Vamos achar Reynolds (Re) e Prandtl (Pr):
A equação de Reynolds é a seguinte:
Onde,
-D é o diâmetro do cilindro;
-V é a velocidade do fluido;
-ν é a viscosidade cinemática do fluido.
Vamos encontrar a viscosidade cinemática pela Tabela A.4
A T=20ºC=293K:
Aplicando os valores
Pela mesma Tabela A.4 achamos o número de Prandtl, Pr, e também o valor de k:
Passo 4
As constantes m e C, podem ser encontradas na Tabela 7.2 do Incropera, cap. 7, pegando o valor de Re encontrado.
Para Re=1,965x104, os valores de C e m que estão na faixa de Re para esse valor é:
Passo 5
Agora é só calcular o h
Aplicando os valores
Passo 6
Agora vamos determinar a resistência térmica da convecção
Pela definição de resistência térmica
Onde para a convecção, a taxa de transferência de calor, qconv, é
Onde,
-AS é a área superficial do objeto que no caso é um tubo cilíndrico;
-ΔT é a diferença de temperatura entre o fluido e a superfície do tubo cilíndrico.
Assim,
Passo 7
Vamos determinar a área superficial AS:
A área superficial do cilindro é dada por
Assim,
Aplicando os valores:
Passo 8
Como já vimos a taxa de transferência de calor por convecção é dada por:
E também
Onde,
Assim,
Aplicando os valores
Passo 9
Para finalizar vamos plotar um gráfico de h vs D e q vs D
Para isso vamos pegar as expressões para cada um em função do diâmetro
Para h:
Na qual, apenas Re que é função do diâmetro
Assim,
Aplicando os valores, exceto o de D:
Passo 10
E para q:
Aplicando os valores, exceto o de D:
Com as expressões de h e q podemos plotar o gráfico de hvsD e qconvvsD
Passo 11
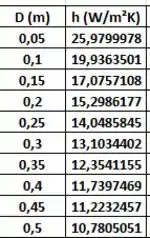
Pelo EXCEL, o gráfico para h vs D foi, com os seguintes dados:
Também pelo EXCEL, o gráfico para qconv vs D foi, com os seguintes dados:
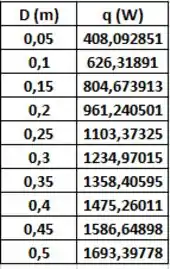
*Observação: Você pode perceber que a taxa de transferência de calor aumenta com o aumento do diâmetro, mas o coeficiente de troca térmica por convecção diminui, sendo que o coeficiente de troca térmica, h, é proporcional a taxa de transferência de calor, q, mas nesse caso, mesmo com a diminuição de h o valor de q aumenta, isso é devido a maior área de troca térmica que o cilindro possui com maior diâmetro. Então, operacionalmente, a dimensão do cilindro, em um processo de fluxo cruzado, é mais significativa do que as condições de escoamento, representado por h.
Resposta
