Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 1.Exercício - Ex. 11

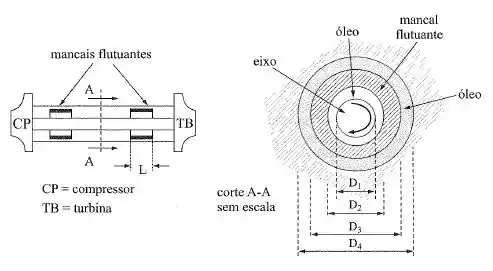
O turbocompressor de um motor de combustão interna tem uma rotação de 120.000   r p m ω = 2 π n . Os mancais do eixo são flutuantes e giram com uma certa rotação. São dados: μ = 8 × 10 - 3   N ⋅ s / m 2 ; D 1 = 12   m m ; D 2 = 12,05   m m ; D 3 = 15,05   m m ; D 4 = 15,1   m m ; L = 20   m m . Na condição de equilíbrio dinâmico, na rotação dada pede-se:

  1. A rotação do mancal flutuante;
  2. O momento resistente à rotação que age no eixo do turbocompressor relativo aos mancais.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

O item a nos pede para determinar a rotação do mancal flutuante. Para esta análise os momentos internos e externos devem ser iguais:

M i n t = M e x t

Desenvolvendo, temos que:

μ v 1 - v 2 ε 1,2 2 π R 2 L R 2 = μ v 3 ε 3,4 2 π R 3 L R 3

Sabemos que:

ε 1,2 = R 2 - R 1

ε 1,2 = 12,05 2 - 12 2

ε 1,2 = 0,025   m m

E:

ε 3,4 = R 4 - R 3

ε 3,4 = 15 , 1 2 - 15,05 2

ε 3,4 = 0,025   m m

Passo 2

Agora podemos desenvolver a relação dos momentos:

v 1 - v 2 ε 1,2 R 2 2 = v 3 ε 3,4 R 3 2

Como descobrimos que:

ε 1,2 = ε 3,4 = 0,025   m m

Teremos que:

v 1 - v 2 v 3 = R 3 2 R 2 2

Passo 3

Vamos chamar de n 2 a rotação do mancal flutuante. Sabendo que esta se associa às velocidades v 2 e v 3 e que:

v = ω ⋅ r

Temos que:

2 π n 1 R 1 - 2 π n 2 R 2 2 π n 2 R 3 = R 3 2 R 2 2

n 1 R 1 - n 2 R 2 n 2 R 3 = R 3 2 R 2 2

Isolando n 2 , temos que:

n 2 = n 1 R 1 R 3 2 R 2 2 R 3 + R 2

Resolvendo, temos que:

n 2 = 120000 12 2 15,05 2 3 12,05 2 2 + 12,05 2

Portanto, a rotação do mancal flutuante será:

n 2 = 40533   r p m

Passo 4

Para o item b, precisamos encontrar o momento resistente à rotação atuante no eixo do turbocompressor relativo aos mancais.

A relação do momento é dada por:

M = 2 τ A 1 D 1 2

Onde:

τ = μ ∆ v ε

E:

A 1 = π D 1 L

Desenvolvendo, temos que:

M = 2 μ ∆ v ε π R D 1 L D 1 2

M = π μ L D 1 2 ε v 1 - v 2

Portanto:

M = π μ L D 1 2 ε π n 1 D 1 - π n 2 D 2

M = π 2 μ L R 1 2 ε n 1 D 1 - n 2 D 2

Substituindo os valores, temos que:

M = 3,14 2 8 × 10 - 3 0,02 0,012 2 0,025 120000 60 0,012 - 40534 60 0,01205

O momento resistente à rotação atuante no eixo do turbocompressor relativo aos mancais será:

M = 0,14   N ⋅ m

Resposta

a )   n 2 = 40533   r p m

b ) M = 0,14   N ⋅ m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o campo de velocidade do Problema 2.20. Trace a linha de emissão formada por partículas que passaram pelo ponto ( 1 ,1 ) durante o intervalo de tempo de t=0 a t=3s . Compare com as linhas de
Um escoamento é descrito pelo campo de velocidade = at + b , em que a=0,4m / 2 e b=2m / s . Em t=2s , quais são as coordenadas da partícula que passou pelo ponto (2, 1) em t = 0? Em t=3s , quais são a
Considere o campo de velocidades V → = a x î + b y ( 1+c t ) j ^ î , em que a = b = 2s - 1 e c = 0,4s - 1 . As coordenadas são medidas em metros. Para a partícula que passa pelo ponto ( x ,y ) =( 1 ,1
CConsidere o campo de escoamento dado na descrição euleriana pela expressão V → = a x î + b y t j ^ î , em que a = 0,2s - 1 , b = 0,04s - 2 e. e as coordenadas são medidas em metros. Deduza as funções
Considere a mangueira de jardim da Figura 2.5. Suponha que o campo de velocidade é dado por V → = u 0 î +v 0 s e n [ ω ( t-x / u 0) ] j ^ î , onde a direção x é horizontal e a origem está na posição m