Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 51

Uma placa de circuitos com uma densa distribuição de circuitos integrados (CI) e dimensões de 120   m m por 120   m m de lado é resfriada pelo escoamento paralelo de ar atmosférico com uma velocidade de 2   m / s .

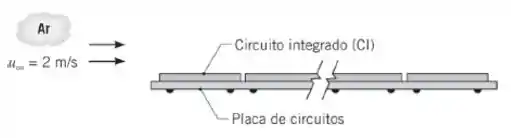
A partir de teste de túnel de vento sob as mesmas condições de escoamento, a tensão cisalhante viscosa média na superfície superior é determinada igual a 0,0625   N / m 2 . Qual é a dissipação de potência admissível na superfície superior da placa se a temperatura superficial média dos CIs não pode exceder a temperatura do ar ambiente em mais de 25 ° C ? Determine as propriedades termofísicas do ar a 300   K .

Passo 1

Pela Analogia modificada de Reynolds, temos que:

C f ¯ 2 = S t ¯   P r 2 3

O coeficiente de atrito é expresso por:

C f ¯ = 2 τ s ¯ ρ u ∞ 2

E o número de Stanton por:

S t ¯ = h ¯ ρ u ∞ c p

Substituindo na Analogia modificada de Reynolds:

1 2 2 τ s ¯ ρ u ∞ 2 = h ¯ ρ u ∞ c p P r 2 3

Isolando h ¯ :

h ¯ = τ s ¯ c p u ∞ P r 2 3

Passo 2

Pela a Tabela A . 4 obteremos as seguintes propriedades para o ar sob a temperatura de 300   K :

c p = 1007   J / k g ⋅ K

P r = 0,707

Dados:

τ s ¯ = 0,0625   N / m 2 ;

u ∞ = 2   m / s .

Substituindo na equação do Passo 1:

h ¯ = 0,0625 ⋅ 1007 2 ⋅ 0,707 2 3

h ¯ = 39,65   W / m 2 ⋅ K

Passo 3

Calculando a dissipação de potência admissível na superfície superior da placa se a temperatura superficial média dos CIs não pode exceder a temperatura do ar ambiente em mais de 25 ° C :

q = h ¯ A s T s - T ∞

Dados:

A s = 120   m m × 120   m m = 0,0144   m 2 ;

T s - T ∞ = 25 ° C = 25   K .

Temos:

q = 39,65 ⋅ 0,0144 ⋅ 25

q = 14,27   W

Resposta

q = 14,27   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o fluxo de ar sobre a superfície de uma placa mantida a uma temperatura de 220 ℃ ℃. O perfil de temperatura do fluxo de ar é dado como: T y =T ∞ - T ∞ -T s e x p -V α f l u i d o y O fluxo d
Durante o resfriamento de batatas ao ar, o coeficiente combinado de transferência de calor por convecção, radiação e evaporação é determinado experimentalmente, desta forma:Considere uma batata de 8c
O coeficiente de perda de calor por convecção para uma pessoa vestida, em pé, no ar em movimento, é expresso como h = 14,8 V 0,69 para 0,15V1,5m / s , em que V é a velocidade do vento. Para uma pessoa
Durante o resfriamento a ar de laranjas, uvas e tangerinas, o coeficiente combinado de transferência de calor por convecção, radiação e evaporação para velocidades do ar de 0,11V0,33m / s é determinad
Considere o escoamento de Couette e um fluido com viscosidade de μ = 0,8 N.s/m2 e condutividade térmica de k f = 0,145 W/m.K. A placa inferior é estacionária e feita de material de condutividade térmi