Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 34

Uma placa fina em formato de triângulo equilátero está imersa paralelamente a um escoamento de 12 m/s de água a 20°C, como na Figura P7.34. Considerando R e t r = 5 × 10 5 , calcule o arrasto sobre essa placa.

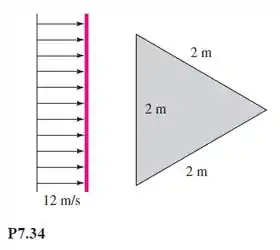
Passo 1

Eeeeee, vamos nessa, cara! Bora mandar ver com essa questão ai!

Cara, bora imaginar a gente tirando uma tirinha de largura dx ao longo de (L-x) paralelo a placa, assim

d A = 2 L - x tan ⁡ 30 ° d x

Em que, L = a sen ⁡ 60 °   e a = 2 m .

Para a parte laminar, temos:

d F l a m i n a r = τ p ρ μ x 1 2 U 3 2 2 L - x tan ⁡ 30 ° d x ( 2   l a d o s )

Integrando de 0 até x c r i t , teremos:

F l a m i n a r = 1,328 ρ μ 1 2 U 3 2 tan ⁡ 30 ° 2 L x c r i t 1 2 - 2 3 x c r i t 3 2

Para a parte turbulenta, temos:

d F t u r b u l e n t o = τ p d A = 0,027 ρ U 2 2 ν U x 1 7 2 L - x tan ⁡ 30 ° d x ( 2   l a d o s )

Integrando de x c r i t até L, teremos:

F t u r b u l e n t o = 0,054   ρ ν 1 7 U 13 7 tan ⁡ 30 ° 7 6 L 13 7 - L x c r i t 6 7 - 7 13 L 13 7 - x c r i t 13 7

Passo 2

A força total será F t u r b u l e n t o + F l a m i n a r . Tendo L = 1,732   m e, para a água, ρ = 998   k g / m 3 e μ = 0,001   k g / ( m ⋅ s ) , vamos calcular x c r i t e F, logo:

R e c r i t = 5 E 5 = ρ U x μ = 998 k g m 3 12 m s x c r i t 0,001 k g m ⋅ s → x c r i t = 0,042   m

Assim, substituindo nas expressões de força, teremos:

F l a m i n a r = 22   N

F t u r b u l e n t o = 703   N

Logo, nossa força total será de:

F t o t a l = F t u r b u l e n t o + F l a m i n a r = 703 + 22 = 725   N

Resposta

F t o t a l = 725   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Repita o Problema 9.44, considerando agora que o escoamento de ar é a 25 m / s (considere escoamento na camada limite turbulenta).
Uma camada limite de ar padrão, em desenvolvimento sobre uma placa plana, é mostrada na Fig 9.18. O escoamento de corrente livre fora da camada-limite não é perturbado com velocidade U = 50m / s . A p
Repita o problema 9.60, usando a expressão do perfil de velocidade de potência 1 / 8 .
Ar-padrão escoa sobre uma placa horizontal plana e lisa, com velocidade de corrente livre U = 20m / s . O comprimento da placa é L = 1,5m e a sua largura é b = 0,8m . O gradiente de pressão é zero. A
Ar na condição padrão escoa sobre uma placa plana. A velocidade de corrente livre 10m / s . Determine δ e τ w em x = 1m , medido a partir da borda de ataque, considerando (a) escoamento completamente