Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 15

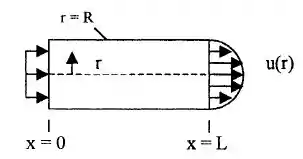
Água, admitida incompressível, escoa em regime permanente pelo tubo como mostra abaixo. A velocidade na entrada é constante, u = U o , e a velocidade na saída se aproxima do perfil para escoamento turbulento, u = u m á x 1 - r R 1 7 . Determine a razão U o / U m á x para esse escoamento.

Passo 1

Fala ae, galerinha!! Tranquilidade? Bora cair dentro de mais um exercício de mecânica os fluidos? LERIGOOOUU!!!!

Bem, primeiro de tudo a gente vai precisar fazer um balanço de massa para nosso escoamento. Considerando um escoamento incompressível, isso quer dizer que ∂ ρ ∂ t = 0 e podemos dizer que temos um escoamento permanente. Isso faz a gente chegar à seguinte conclusão: O que entra é igual ao que sai, ou seja, vazão de entrada é igual a vazão de saída.

Q 1 = Q 2

Passo 2

A gente agora tem que lembrar como se calcula vazão, certo? Vazão é dada pelo produto entre área transversal e velocidade média do escoamento.

Então aí vem o grande pulo do gato!!!! Toda vez que sua velocidade média for igual a um VALOR constante, você só precisa multiplicar ele pela área transversal do escoamento. Toda vez que você tiver um PERFIL DE VELOCIDADE, precisará integrar ele na área transversal de escoamento.

Passo 3

Então bora fazer o que falamos no passo 2, beleza?

Q 1 = Q 2

U 0 A 1 = ∫ u   d A

Agora é a gente lembrar do seguinte: a área transversal de escoamento é um círculo, certo? Então precisamos lembrar de transformar a nossa diferencial da área em coordenadas cilíndricas!!! OMGGGGGG E AGORA??

Calma, é bem tranquilo!!! Toda vez que você observar que a área transversal de um escoamento é um círculo, pega a diferencial da área e escreve ela como sendo r d r d θ

U o A 1 = ∫ 0 2 π ∫ 0 R u   r d r d θ

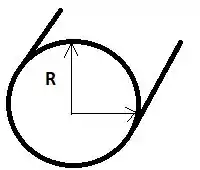
Nosso ângulo varia e 0 até 2 π , certo? E o raio varia de 0 até R, show de bola?

U 0 π R 2 = ∫ 0 R u m á x 1 - r R 1 7 2 π r d r

U 0 π R 2 = 2 π u m á x ∫ 0 R r - r 2 R 1 7 d r

U 0 π R 2 = u m á x 49 π 60 R 2

U 0 u m á x = 49 60

Resposta

U 0 u m á x = 49 60

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um tanque e ar altamente pressurizado nas condições p 0 ,ρ 0 ,T 0 e volume v 0 . No capítulo 9 aprenderemos que, se deixarmos o tanque descarregar para a atmosfera através de um bocal conver
Uma fina camada de líquido escorrendo sobre um plano inclinado, como mostra a seguir, terá um perfil de velocidades laminar, u ≈ U o 2 y h - y 2 h 2 , em que U o é a velocidade na superfície. Se o pla
Um fluido incompressível escoa em regime permanente pelo duto retangular da figura a seguir. O perfil de velocidades na saída é dado aproximadamente por u = u m á x 1 - y 2 b 2 1 - z 2 h 2 á (a) Esse
O escoamento permanente incompressível entre placas paralelas tem velocidade uniforme na entrada u = U o = 8c m / s , desenvolvendo-se a jusante num perfil laminar parabólico, u = a z z o - z , em que
Modifique o problema P3.16 da seguinte maneira: Considere que a placa tenha comprimento L = 125 δ da entrada até a saída. A placa é porosa e está retirando fluido da camada-limite a uma velocidade de