Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 10.Problemas - Ex. 73
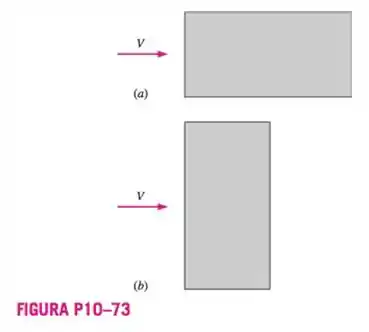
Uma dimensão de uma placa retangular é o dobro da outra dimensão. O ar a uma velocidade uniforme flui paralelo à placa e uma camada limite laminar se forma em ambos os lados da placa. Qual a orientação – dimensão mais longa paralela ao vento (Figura P10-73a) ou dimensão mais curta paralela ao vento (Figura P10-73b) – apresenta um arrasto maior? Explique.
Passo 1
Tá legal! Conforme vimos no exercício 10-72 ou no exemplo 10 desta seção, a equação para a tensão de cisalhamento é dada por:
E, sabemos que a força de arrasto pode ser dada pela multiplicação dessa tensão pela área da placa. No entanto, conforme foi dito no enunciado, as placas possuem a mesma área superficial. Então, nesse caso precisamos olhar somente para a tensão de cisalhamento .
Passo 2
Então, podemos ver que depende da densidade , da velocidade e do número de Reynolds . Para a nossa análise, a única variável que temos é o número de Reynolds, pois os outros dois valores serão constantes para as duas placas. Então, sabendo que o número de Reynolds é dado por:
Novamente, e serão constantes para as duas placas, e que irá mudar será o comprimento , que é medido paralelo à direção do escoamento. Então, o caso (a), com um comprimento maior, terá um Reynolds maior, e o caso (b), com um comprimento menor, terá um Reynolds maior. Com isso, como a tensão de cisalhamento é inversamente proporcional ao número de Reynolds, quanto menor ele for, maior será a tensão de cisalhamento.
Passo 3
E, com uma tensão de cisalhamento maior, como por sua vez ela é diretamente proporcional à força de arrasto, então, a força de arrasto também será maior. Então, no nosso caso, a placa (b) terá uma força de arrasto maior.
Resposta
(b).