Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 66

Uma esfera de massa específica ρ e e diâmetro D cai em um fluido de massa específica ρ e viscosidade μ , partindo do repouso. Admitindo um coeficiente de arrasto constante C A o , deduza uma equação diferencial para a velocidade de queda V ( t ) e mostre que a solução é:

V = 4 g D d - 1 3 C A o 1 2 tanh ⁡ C t

C = 3 g C A o d - 1 4 S 2 D 1 2

Em que d = ρ e / ρ é a densidade do material da esfera.

Passo 1

E aí, gente!! Tudo bem? Vamos encarar juntos mais um desafio de mecflu? Então boraaaa!!!!

Antes de mais nada, vamos desenhar nosso problema pra entender o que está acontecendo!

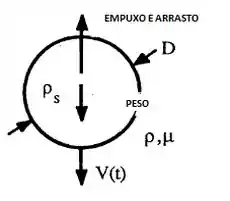
É importante dizer que o problema diz que a esfera parte do repouso, mas ela não está em repouso, ou seja, o somatório das forças tem que ser igual a massa dela vezes a aceleração, certo?

W - E - A = m   a

Onde W = f o r ç a   p e s o ,   A = f o r ç a   d e   a r r a s t o ,   E = e m p u x o

Passo 2

Vamos agora abrir nossa equação, beleza? Vamos explicitar a força de arrasto, a massa, e a aceleração!!!

W - E - C D ρ 2   V 2 A = W g d V d t

Onde sabemos que a nossa área é dada por: π 4 D 2

W - B = ρ S - 1 g π 6 D 3

Vamos rearranjar as paradas de forma a obtermos d V d t = β - α V 2

β = g 1 - 1 S                     α = ρ g C D A 2 W

Passo 3

Agora é só separarmos as variáveis e integrarmos!!

∫ d t = ∫ d V β - α V 2

V = β α tanh ⁡ t α β = V f i n a l tanh ⁡ C t

Onde V f i n a l = 4 g D S - 1 3 C D 1 2 e também que C = 3 g C D S - 1 4 S 2 D 1 2

Resposta

V = β α tanh ⁡ t α β = V f i n a l tanh ⁡ C t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um paraquedista salta de um avião, usando um paraquedas de 8,5 m de diâmetro na atmosfera padrão. A massa total do paraquedista e do paraquedas é 90 kg. Admitindo um paraquedas aberto e movimento quas
Um tanque de sedimentação para abastecimento municipal de água tem 2,5 m de profundidade, e a água a 20°C escoa continuamente a 35 cm/s. Calcule o comprimento mínimo do tanque para garantir que todo o
Uma chaminé ao nível do mar tem 2 m de diâmetro e 40 m de altura. Quando está sujeita a ventos fortes de 80 km/h, qual é o momento fletor induzido pelo vento em relação à base da chaminé?
O cabo transversal principal entre as torres de uma ponte pênsil litorânea tem 60 cm de diâmetro e 90 m de comprimento. Calcule a força total de arrasto sobre esse cabo com ventos laterais de 80 km/h.
A dedução da Equação (7.42) para δ / x no escoamento turbulento empregou correlações de velocidade bem simples, Equações (7.38) e (7.39). Uma lei de parede unificada foi dada por Spalding [54]: y + =