Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 21

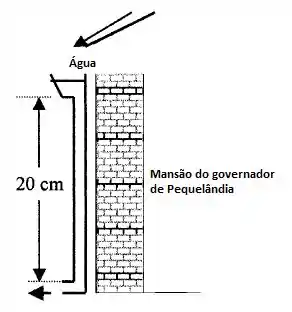
Em Pequelândia, as casas tem menos de 30 cm de altura! A chuva cai em regime laminar! O tubo de drenagem da figura abaixo tem apenas 2 mm de diâmetro. (a) Quando a calha está cheia, qual é a taxa de drenagem? (b) A calha é projetada para uma tempestade súbita de até 5 mm por hora. Nessa condição, qual é a máxima área de telhado que pode ser drenada com sucesso? (c) Qual é o valor de R e d ?

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!

Se a velocidade na calha (na superfície da calha) for negligenciada, a equação de energia pode ser reduzida como?

p 1 ρ g + V 1 2 2 g + z 1 = p 2 ρ g + V 2 2 2 g + z 2 + h f

Se p 1 = p 2 = p a t m e V 1 ≈ 0 , onde o ponto 1 é a parte superior da calha por onde entra água da chuva e o ponto 2 é a saída do tubo que leva essa água, temos que:

Δ z = V 2 2 2 g + h f

Passo 2

Como sabemos que o escoamento será laminar, temos que:

Δ z = V 2 2 2 g + h f = V 2 2 2 g + 32 μ L V ρ g d 2

Note que temos V 2 = V , pois a velocidade de saída no ponto 2 é igual a velocidade do fluido dentro do tubo, pois na iminência de sua saída do mesmo, a velocidade ainda será a mesma ao longo do tubo, uma vez que sua seção transversal de escoamento não foi alterada.

Passo 3

Substituindo os valores de ρ = 998   k g / m ³ , μ = 0,001   k g / ( m . s )  

(a) Com a variação de altura Δ z conhecida, a equação ficará quadrática em V, certo?

0,2 = V 2 2 9,81 + 32 0,001 0,2 V 998 9,81 0,002 2

0,051 V 2 + 0,1634 V - 0,2 = 0

Temos duas raízes, onde apenas a positiva tem interesse e sentido físico pra gente!

V = - b + b 2 - 4 a c 2 a = - 0,1634 + 0,1634 2 + 4 0,051   x   0,2 2 ( 0,051 ) = 0 , 945   m / s

Passo 4

Ou seja, nossa vazão supondo escoamento laminar é dada por:

Q = A V = π 4 d 2 V = π 4 0,00 2 2 0 , 945 = 3   x   10 - 6 m 3 s = 0,0107 m 3 h

Passo 5

(b) A área de drenagem que terá sucesso deve ser calculada como sendo:

0,0107 m 3 h 0,005 m h = 2,14   m ²

Passo 6

(c) O número de Reynold na calha é calculado como sendo:

R e = ρ V d μ = 998 0,945 0,002 0,001 = 1890   ( L a m i n a r )

Resposta

  1. 0,0107 m 3 h
  2. A d r e n a g e m = 2,14   m 2
  3. R e = 1890  
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água é descarregada para a atmosfera a partir de um grande tanque, em regime permanente e através de um trecho de tubo de plástico liso. O diâmetro interno do tubo é 3,18 mm e seu comprimento é 15,3 m
Um difusor cônico é usado para expandir um tubo de um diâmetro de 100 mm para um diâmetro de 150 mm. Determine o comprimento mínimo do difusor, se desejamos um coeficiente de perda (a) K d i f u s o r
Analise o escoamento através de uma expansão súbita para obter uma expressão para a velocidade média V - 1 em termos da variação de pressão ∆ p = p 2 - p 1 , da razão de áreas R A , da massa específic
Considere novamente o escoamento através do cotovelo analisado no Exemplo 4.6. Usando as condições dadas, calcule o coeficiente de perda menor para o cotovelo.
Água escoa do tanque mostrado através de um tubo muito curto. Considere que o escoamento seja quase permanente. Estime a vazão no instante mostrado. Como você poderia melhorar o sistema de escoamento