Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 127

Reconsidere o Problema 3-126. Usando o EES (ou um outro aplicativo), investigue o efeito da aceleração sobre a inclinação da superfície livre da água do tanque. Faça a aceleração variar de 0   m / s 2   até 5   m / s 2 em incremento de 0,5   m / s 2 . Tabule e mostre graficamente os resultados.

Passo 1

Bora láaaa! Primeiro vamos rever um esqueminha do exercício anterior!

Além disso, temos as equações consideradas na resolução anterior:

tan ⁡ θ = a x g

Δ y m á x = L 2 tan ⁡ θ

h m á x = h 0 + Δ y m á x

Substituindo:

h m á x = h 0 + L 2 tan ⁡ θ

P m á x = P 1 = ρ H 2 O g h m á x

O enunciado ta pedindo pra investigar o efeito da aceleração sobre a inclinação que a supefície da água vai fazer no tanque ! Vamos nessa então!

Passo 2

Com o EES aberto a gente vai colocar os dados e as fórmulas que a gente falou no Passo 1! Beleza?!

Vai ficar assim:

Com esses dados a gente já pode montar a nossa tabela! Para isso a gente vai selecionar as variáveis, a x ,   h m á x ,   P m á x   e θ .

Fica assim:

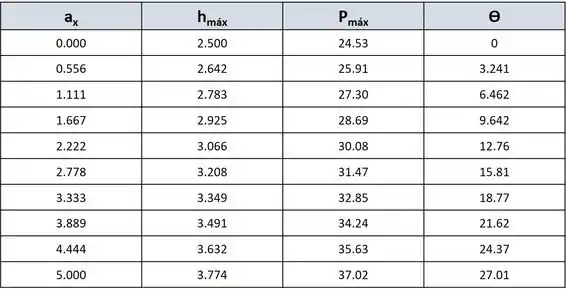
Passo 3

Agora podemos plotar o gráfico!

No eixo x vai ficar a aceleração a x e no eixo y o ângulo θ . Plotando o gráfico ele fica assim:

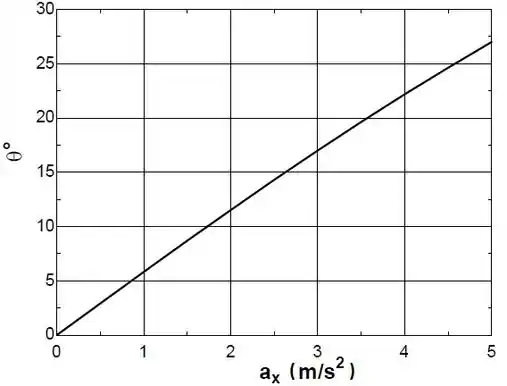
Fechooou!

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro vertical vedado com 1,2 m de diâmetro e 3 m de altura é preenchido completamente com gasolina, cuja densidade é de 740 kg/m³. Agora o tanque é posto a girar em torno de seu eixo vertical a
Repita o Problema 3-88 para uma desaceleração de 2,5 m/s².
A distância entre os centros dos dois braços do tubo em U aberto para a atmosfera é de 25 cm e o tudo em U contém 20 cm de altura de álcool em ambos os braços. Agora o tubo em U é posto para girar em
O painel ABC no lado inclinado de um tanque de água é um triângulo isósceles com vértice em A e a base BC = 2 m como mostrado abaixo. Determine a força de água sobre o painel e sua linha de ação.
Na figura abaixo, a comporta AB tem 1,5 m de largura e o limitador B irá quebrar se a força da água for igual a 41000 N. Para qual profundidade de água essa condição é alcançada?