Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 69

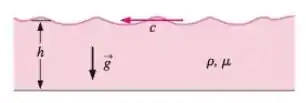
Use a análise dimensional para mostrar que em um problema envolvendo ondas em água rasa (Figura P7-69), tanto o número de Froude quanto o número de Reynolds são parâmetros adimensionais relevantes. A velocidade c das ondas da superfície de um líquido é função da profundidade, da aceleração gravitacional g , da densidade do fluido ρ e da viscosidade do fluido μ . Manipule seus Π ’s para obter os parâmetros na seguinte forma:

F r = c g h = f R e                                 o n d e   R e = ρ c h μ

Passo 1

Vamos começar escrevendo a velocidade das ondas em relação aos termos envolvidos no problema:

c = f h , ρ , μ , g                 n = 5  

Escrevendo esses parâmetros em termos das dimensões primárias, temos:

c → L 1 t - 1

h → L 1

ρ = m 1 L - 3

μ = m 1 L - 1 t - 1

g = L 1 t - 2

Vamos definir j = 3 , o número de dimensões primárias que estão representadas no problema. Assim, o número de grupos adimensionais Π é:

k = n - j = 5 - 3 = 2

Passo 2

Vamos escolher três parâmetros que se repetem, geralmente um parâmetro geométrico, um cinemático e um dinâmico

h ,   g   e   ρ

Com isso os números Π podem ser expressos como:

Π 1 = c h a ρ b g c → Π 1 = L 1 t - 1   L 1 a m 1 L - 3 b L 1 t - 2 c

Π 2 = μ h d ρ e g f → Π 2 = { ( m 1 L - 1 t - 1 )   L 1 d m 1 L - 3 e L 1 t - 2 f

Para o primeiro número Π temos:

Massa:

m 0 = m b → b = 0

Comprimento:

L 0 = L 1 L a L - 3 b L c → 0 = 1 + a - 3 b + c → a = - 1 - c

Tempo:

t 0 = t - 1 t - 2 c → 0 = - 1 - 2 c → c = - 1 2

a = - 1 2

Assim:

Π 1 = c h - 1 / 2 ρ 0 g - 1 / 2 = c g h = F r

Para Π 2 :

Massa:

m 0 = m 1 m b → b = - 1

Comprimento:

L 0 = L 1 L a L - 3 b L c → 0 = 1 + a - 3 b + c → a = - 1 + 3 - c → a = 2 - c

Tempo:

t 0 = t - 1 t - 2 c → 0 = - 1 - 2 c → c = - 1 2

a = - 3 2

Logo:

Π 2 = μ h - 3 / 2 ρ - 1 g - 1 / 2 = μ ρ h 3 2 g

Passo 3

Vamos manipular os números Π de forma a relacionar Π 1 e Π 2 . Em Π 2 temos:

Π 2 = μ ρ h 3 2 g = μ ρ h h g =   μ ρ h g h

Se invertemos essa relação e multiplicarmos por F r , vamos obter:

Π 2 =   ρ h g h μ   c g h = ρ c h μ = R e

Assim a relação entre os números Π pode ser representada por

F r = c g h = f R e         o n d e   R e = ρ c h μ

Visto que o número de Reynolds está relacionado com a velocidade de onda e, dessa forma, o número de Froude pode ser representado em função do número de Reynolds.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O número de Stanton é listado como um parâmetro adimensional nomeado e usual na Tabela 7-5. Entretanto, uma análise cuidadosa revela que, na verdade, ele pode ser formado por uma combinação entre o nú
Um precipítador eletrostátíco (ESP) é um dispositivo usado em diversas aplicações para limpar o ar carregado de partículas. Em primeiro lugar, o ar empoeirado passa através do estágio de carga do ESP,
Muitos dos parâmetros adimensionais usuais listados na Tabela 7-5 podem ser formados pelo produto ou razão de dois outros parâmetros adimensionais usuais. Para cada par de parâmetros adimensionais lis
Quando um tubo capilar de diâmetro pequeno D é inserido em um contêiner de líquido, o líquido se eleva até a altura h dentro do tubo (Figura). h é uma função da densidade do líquidop, do diâmetro do t
Considere uma variação do problema do escoamento de Couette completamente desenvolvido do Problema 7-52 — o escoamento entre duas placas paralelas finitas separadas pela distância h , com a placa supe