Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 47

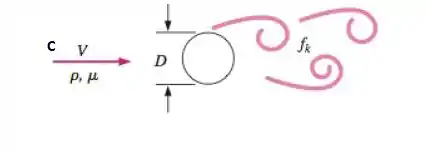
Repita o problema 7-46, mas com um parâmetro independente adicional incluído: a velocidade do som c no fluido. Use o método de várias variáveis repetidas para gerar uma relação adimensional para a frequência de emissão de vórtices de Kármán fk como função da velocidade da corrente livre V, da densidade do fluido ρ, da viscosidade do fluido µ, do diâmetro do cilindro D e da velocidade do som c. Mostre todo seu trabalho.

Passo 1

O problema diz que temos 5 parâmetros, certo? Portanto n = 6

Então, vamos primeiro escrever esses parâmetros!!!

h = f ( V , ρ ,   μ ,   D , c )

Passo 2

Vamos agora escrever as dimensões primárias pra cada variável!!

f k = t - 1

V = L t - 1

ρ = M L - 3

μ = m L - 1 t - 1

D = L

c = L t - 1

Passo 3

Agora a gente vai ter que pegar o número de varíaveis e diminuir pela quantidade de dimensões primárias que usamos, ou seja, MLt, então temos 3!!

Vamos chamar de k essa diferença e j a quantidade de dimensões primárias, se liga!

k = n - j = 6 - 3 = 3

Esse número k diz o QUANTOS NÚMEROS ADIMENSIONAIS TEREMOS/ESPERAMOS TER!

Passo 4

Precisamos agora escolher três parâmetros que juntos, precisam formar uma combinação das 3 dimensões usadas.

Vamos escolher aqui: V ,   ρ   e   D

Passo 5

Agora se liga, vamos encontrar os grupos π ' s (grupos pi) e pra isso queremos saber quais são seus expoentes. Olha como a gente vai fazer isso:

π 1 = f k V a ρ b D c

Agora a gente vai abrir esses parâmetros com suas dimensões básicas lá do passo 2.

π 1 = t - 1 L t - 1 a M L - 3 b L c

Vamos fazer agora um sisteminha com essas variáveis de acordo com seus expoentes e igualando a zero SEMPRE!

Sabendo b e a, calculamos c:

M → b = 0

t → - 1 - a = 0 → a = - 1

L → a - 3 b + c → c = 1

Dessa forma, π 1 = f k D V = S t → N ú m e r o   d e   S t r o u h a l

Vamos fazer a mesma coisa pra encontrar o grupo π 2 com as 4 variáveis agora que descrevem h!

π 2 = μ V a ρ b D c

Agora a gente vai abrir esses parâmetros com suas dimensões básicas lá do passo 2.

π 2 = ( m L - 1 t - 1 ) L t - 1 a M L - 3 b L C

Vamos fazer agora um sisteminha com essas variáveis de acordo com seus expoentes e igualando a zero SEMPRE!

M → 1 + b = 0 → b = - 1

t →   - 1 - a = 0 → a = - 1

L → - 1 + a + 3 b + c = 0 → c = 1 + 1 - 3 = - 1

Dessa forma, π 2 = μ ρ V D → π 2 - 1 = R e

Podemos escrever então que a relação é dada por S t = f ( R e )

Passo 6

O terceiro grupo será dado por:

π 3 = c V a ρ b D c = L t - 1 L t - 1 a M L - 3 b L c

M → b = 0

t → - 1 - a = 0 → a = - 1

L → 1 + a - 3 b + c = 0 → c = 0

π 3 = V c = M a → N ú m e r o   d e   M a c h  

Podemos escrever ao final que:

S t = f ( R e , M a )

Resposta

S t = f ( R e ,   M a )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Defina o bloqueio do túnel de vento. Qual é a regra prática ao bloqueio máximo aceitável para um teste de túnel de vento? Explique por que haveria erros de medição se o bloqueio fosse significativamen
A taxa de transferência de calor para a água que escoa em um tubo foi analisada no Problema 7-20. Vamos abordar esse mesmo problema, mas agora com a análise dimensional. A água fria entra em um tubo,
Considere o escoamento laminar através de uma seção longa do tubo, como na Figura P7-62. Para escoamento laminar a rugosidade da parede não é um parâmetro relevante, a menos que ε seja muito grande. A
Considere novamente o exemplo da carreta modelo discutido na Seção 7 - 5 , exceto que a velocidade máxima do túnel de vento é de apenas 50m / s . Os dados da força aerodinâmica são obtidos para as vel
Considere o escoamento de Poiseouille e bidimensional, laminar desenvolvido, — o escoamento entre duas placas paralelas finitas separadas pela distância h , com a as placas superior e inferior fixas,