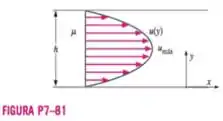
Considere o escoamento de Poiseouille e bidimensional, laminar desenvolvido, — o escoamento entre duas placas paralelas finitas separadas pela distância , com a as placas superior e inferior fixas, e um gradiente de pressão forçado movendo o escoamento, como ilustra a Figura . ( é constante e negativo). O escoamento é incompressível, e bidimensional no plano . O escoamento também é completamente desenvolvido, significando que o perfil de velocidade não varia com a distância a jusante, . Devido à natureza copletamente desenvolvida do escoamento, não há efeitos inerciais e a densidade não entra no problema. Acontece que , o componente da velocidade na direção , é uma função da distância , do gradiente de pressão , da viscosidade do fluido e da coordenada vertical . Faça uma análise dimensional (mostrando todo o seu trabalho) e gere uma relação adimensional entre as variáveis dadas.

Vamos lá, o primeiro passo consiste em listar os parâmetros. Existem parâmetros nesse problema, são eles:

No segundo passo, temos as seguintes dimensões primárias dos parâmetros:

No terceiro passo, como primeira tentantiva tomamos que corresponde a quantidade de dimensões primárias do problema . Se este valor de , estiver certo, o numero de esperado é

No quarto passo, nós precisamos escolher parametros repetidos. Não podemos escolher e pois eles tem as mesmas dimensões. Assim, a nossa opção é:

No quinto passo, geramos o primeiro com a variável dependente:

Calculando os expoentes para cada dimensão:

Massa:

Tempo:

Comprimento:

Resolvendo o sisteminha:

Consequentemente, .

Substituindo no :

No sexto passo, nós precisamos gerar o independente, para isso usamos os parametros repetidos, que são os que nos restaram:

Assim, nós podemos unir todos os da seguinte forma:

Prontinho!!