Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 72

Considere novamente o exemplo da carreta modelo discutido na Seção , exceto que a velocidade máxima do túnel de vento é de apenas . Os dados da força aerodinâmica são obtidos para as velocidades do túnel de vento entre e — assuma para essas velocidades os mesmos dados listados na Tabela . Com base apenas nesses dados, os pesquisadores podem ter certeza de terem atingido a independência do número de Reynolds?

Passo 1

Bom, gente, aqui nesse problema nós iremos descobrir se os pesquisadores atingiram a independência do número de Reynolds, ou seja, se o número de Reynolds se estabilizou.

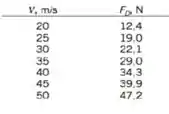
Vamos apenas calcular o coeficiente de arrasto e o número de Reynolds para as velocidades de , e de acordo com a Tabela que o livro propôs:

Passo 2

Vamos considerar os dados do exemplo da Seção . Para , temos:

Agora, para :

E, por fim, para :

Passo 3

A partir dos cálculos anteriores, perceba como os valores do coeficiente de arrasto parece se estabilizar. Esses pontos são expressos pela Figura do livro:

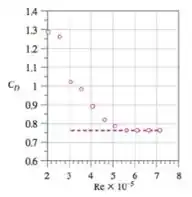
Isso facilita nossa visualização para ver a bagunça que “acontece”. Portanto, entre e , os pesquisadores não conseguem determinar é possível atingir a independência numérica de Reynolds.

Prontinho!!

Resposta

Entre e , os pesquisadores não conseguem determinar é possível atingir a independência numérica de Reynolds.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um teste de modelo de um conjunto cavalo-reboque é realizado em um túnel de vento. A força de arrasto, F D , é considerada ser dependente da área frontal, A , da velocidade do vento, V , da massa espe

Considere novamente o Problema 7.51. A experiência mostra que, para hélices de navios, os efeitos viscosos são pequenos sobre as transposições por escala. Também, quando a cavitação não está presente,

Sobre uma determinada faixa de velocidades do ar, V , a sustentação, F T , produzida por um modelo de uma aeronave completa em um túnel de vento, depende da velocidade do ar, da massa específica do ar

Um modelo em escala 1/10 de um conjunto cavalo-reboque é testado em um túnel de vento. A área frontal do modelo é A m = 0,1m 2 . Quando testado a V m = 75m / s em ar-padrão, a força de arrasto medida

Um modelo de hélice de 1 m de diâmetro é testado em um túnel de vento. O ar aproxima-se da hélice a 50 m/s quando ela gira a 1800 rpm. O empuxo e o torque medidos sob estas condições são 100 N e 10 Nm