Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 45

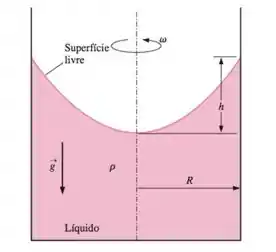
Considere o caso no qual o contêiner e o líquido do Problema 7-44 estão inicialmente em repouso. Em t = 0, o contêiner começa a girar. É preciso algum tempo para que o líquido gire como um corpo rígido e esperamos que a viscosidade do líquido seja um parâmetro adicional relevante no problema não permanente. Repita o Problema 7-44, mas com dois parâmetros independentes adicionais incluídos: a viscosidade do fluido µ e o tempo t. (Estamos interessados no desenvolvimento da altura h como função do tempo e dos outros parâmetros.)

Passo 1

O problema diz que temos 7 parâmetros, certo? Portanto n =7

Então, vamos primeiro escrever esses parâmetros!!!

h = f ( w , ρ , g , R , t ,   μ )

Passo 2

Vamos agora escrever as dimensões primárias pra cada variável!!

h = L

w = t - 1

ρ = M L - 3

g = L t - 2

R = L

t = t

μ = m L - 1 t - 1

Passo 3

Agora a gente vai ter que pegar o número de varíaveis e diminuir pela quantidade de dimensões primárias que usamos, ou seja, MLt, então temos 3!!

Vamos chamar de k essa diferença e j a quantidade de dimensões primárias, se liga!

k = n - j = 7 - 3 = 4

Esse número k diz o QUANTOS NÚMEROS ADIMENSIONAIS TEREMOS/ESPERAMOS TER!

Passo 4

Precisamos agora escolher três parâmetros que juntos, precisam formar uma combinação das 3 dimensões usadas.

Vamos escolher aqui: w ,   ρ   e   R

Passo 5

Agora se liga, vamos encontrar os grupos π ' s (grupos pi) e pra isso queremos saber quais são seus expoentes. Olha como a gente vai fazer isso:

π 1 = h w a ρ b R c

Agora a gente vai abrir esses parâmetros com suas dimensões básicas lá do passo 2.

π 1 = L t - 1 a M L - 3 b L C

Vamos fazer agora um sisteminha com essas variáveis de acordo com seus expoentes e igualando a zero SEMPRE!

L → 1 - 3 b + c = 0

t → - a = 0 → a = 0

M → b = 0

Sabendo b e a, calculamos c:

c = 3 b - 1 = - 1

Dessa forma, π 1 = L R - 1 = L R

Vamos fazer a mesma coisa pra encontrar o grupo π 2 com as 4 variáveis agora que descrevem h!

π 2 = g w a ρ b R c

Agora a gente vai abrir esses parâmetros com suas dimensões básicas lá do passo 2.

π 2 = L t - 2 t - 1 a M L - 3 b L C

Vamos fazer agora um sisteminha com essas variáveis de acordo com seus expoentes e igualando a zero SEMPRE!

L → 1 - 3 b + c = 0

t → - 2 - a = 0 → a = - 2

M → b = 0

Sabendo b e a, calculamos c:

c = 3 b - 1 = - 1

Dessa forma, π 1 = g w - 2 R - 1 = g w 2 R

Vamos modificar o grupo π 2 = F r = w R g R onde Fr é o número de Froude.

Outro grupo pode ser obtido lembrando do seguinte: O 3º grupo será formado com o tempo. Repetindo o parâmetro w e lembrando que tem dimensão t-1, e é o único que fica no grupo. Portanto sem o algebrismo formalmente, temos: π 3 = w t

Passo 6

π 1 = μ w a ρ b R c

Agora a gente vai abrir esses parâmetros com suas dimensões básicas lá do passo 2.

π 1 = M L t - 1 t - 1 a M L - 3 b L C

Vamos fazer agora um sisteminha com essas variáveis de acordo com seus expoentes e igualando a zero SEMPRE!

L → - 1 - 3 b + c = 0

t → - 1 - a = 0 → a = - 1

M → 1 + b = 0 → b = - 1

Sabendo b e a, calculamos c:

c = 1 + 3 b → c = - 2

Dessa forma, π 4 = μ ρ w R 2 → π 4 - 1 = R e

Ao final, podemos dizer que:

h R = f ( F r ,   w t ,   R e )

Resposta

π 1 = h R

π 2 = w R / g R

π 3 = w t

w 4 = μ ρ w R 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A queda de pressão ∆ P = P 1 - P 2 através de uma secção longa de um tubo redondo pode ser escrita em termos da tensão de cisalhamento τ w ao longo da parede. A tensao de cisalhamento que age na pared
O líquido escoa por um orifício na parte inferior de um tanque como mostra a figura abaixo. Considere o caso no qual o orifício é muito pequeno comparado ao tanque ( dD ) . As experiências revelam que
Em muitos circuitos elétricos nos quais algum tipo de escala de tempo está envolvido, como filtros e circuitos de temporizaçào (Figura— um filtro passa baixo), você pode ver um resistor (R) e um capac
Da eletrônica fundamental, sabemos que o escoamento de corrente através de um capacitor em determinado instante é igual à capacitância vezes a taxa de variação da voltagem no tempoatravés do capacitor
Quais são as dimensões primárias da carga elétrica q, sendo que as suas unidades são coulombs (C)? (Sugestão: procure a definição fundamental de corrente elétrica.)