Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 10.Exercício - Ex. 1

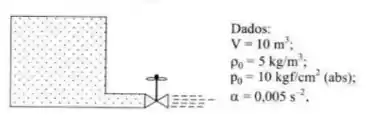
Um reservatório contém um gás e tem uma válvula que controla a sua saída de forma que a pressão interna seja reduzida segundo a lei:

p = p 0 ( 1 - α t 2 )

Sabe-se que durante a descarga a temperatura do gás do reservatório mantém-se constante (processo isotérmico: p ρ = c t e ) e que no instante t = 10   s a passagem de abertura da válvula tem uma área de 0,5   m 2 . Determinar para o instante t = 10   s .

  1. Vazão em massa do gás
  2. A vazão em volume.
  3. A velocidade média na seção de saída
  4. A massa do gás que resta no reservatório
  5. O tempo de esvaziamento do reservatório
  6. A massa do gás no reservatório após o esvaziamento
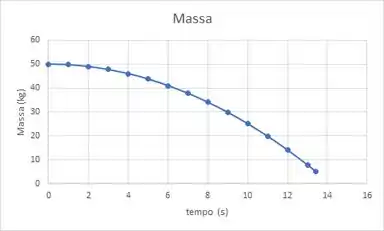
  7. Traçar a curva de esvaziamento do reservatório m=m(t) e verificar que a área abaixo da curva representa a massa que sai até o instante considerado.

Passo 1

Item A)

A questão afirma que:

p ρ = c t e

Assim, a razão entre pressão e densidade em um instante qualquer é igual a razão no instante inicial:

p ρ = p 0 ρ 0

Substituindo a equação: p = p 0 ( 1 - α t 2 )

p 0 ( 1 - α t 2 ) ρ = p 0 ρ 0

Reorganizando obtemos uma fórmula para a densidade:

ρ = ρ 0 ( 1 - α t 2 )

Agora, vamos adotar um volume de controle que represente todo o reservatório

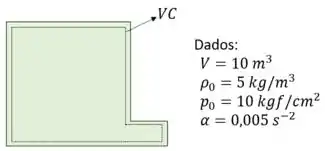
Agora vamos aplicar a equação do volume de controle:

∂ ∂ t ∫ V C ρ ⋅ d V + ∫ S C ρ ⋅ v → × n → ⋅ d A = 0

Como os gases tendem a ocupar todo o volume disponível, então a variação de densidade não depende da variação de volume, nem da variação de área. Então, resolvendo as integrais:7 ∂ ∂ t ρ ∫ V C d V + ρ ⋅ v → × n → ⋅ ∫ S C d A = 0

∂ ∂ t ( ρ ⋅ V ) + ρ ⋅ v → × n → ⋅ A = 0

Já a expressão: ρ ⋅ v → × n → ⋅ A ; corresponde a vazão em massa do sistema:

∂ ∂ t ( ρ ⋅ V ) + Q m = 0

Substituímos a equação da densidade:

∂ ∂ t ( ρ 0 ( 1 - α t 2 ) ⋅ V ) + Q m = 0

Resolvendo:

ρ 0 - 2 α t ⋅ V + Q m = 0

Isolando a vazão em massa:

Q m = 2 α ρ 0 V ⋅ t

Aplicando os valores:

Q m = 2 ⋅ 0,005   s - 2 ⋅ 5 k g m 3 ⋅ 10   m 3 ⋅ 10   s

Q m = 5 k g s

Passo 2

Item B)

No instante t = 10 a densidade é:

ρ = ρ 0 1 - α t 2 = 5 1 - 0,005 ⋅ 10 2 ⇒ ρ = 2,5 k g m 3

A vazão volumétrica é dada por:

Q = Q m ρ

Em t = 10

Q = 5 k g s 2,5 k g m 3  

Q = 2 m 3 s

Passo 3

Item C)

A velocidade é dada por:

v = Q A

Em t = 10

v = 2 m 3 s 0,5   m 2

v = 4 m s

Passo 4

Item D)

A massa no reservatório é dada por:

m = ρ V

Em t = 10

m = 2,5 k g m 3 ⋅ 10   m 3

m = 25   k g

Passo 5

Item E)

O ar vai parar de sair quando a pressão do reservatório for igual a pressão atmosférica p a t m = 10 5   P a = 1 k g f c m 2 . Pela expressão dada pela questão:

p = p 0 1 - α t 2

Em t = 10

1 k g f c m 2 = 10 k g f c m 2 1 - 0,005 ⋅ t 2

Isolando o t:

t = 1 0,005 1 - 1 k g f c m 2 10 k g f c m 2

t = 13,4   s

Passo 6

Item F)

O esvaziamento se dá quando t = 13,4   s . Vamos determinar a densidade neste momento e depois calculamos a massa. Como já deduzimos, a expressão que rege a densidade é:

ρ = ρ 0 1 - α t 2

Aplicando para t = 13,4   s

ρ f i n a l = 5 1 - 0,005 ⋅ 13,4 2

ρ f i n a l = 0,51 k g m 3

E a massa é determinada por:

m f i n a l = ρ f i n a l ⋅ V

m f i n a l = 0,51 ⋅ 10

m f i n a l = 5,1   k g

Passo 7

Vamos determinar uma fórmula pra variação de massa. Sabemos que pra qualquer instante, a densidade é determinada por duas fórmulas:

ρ = ρ 0 1 - α t 2

ρ = m V

Então, para o instante inicial:

ρ 0 = m 0 V

E a massa inicial é:

m 0 = ρ 0 V = 5 ⋅ 10 ⇒ m 0 = 50   k g

Então:

ρ = ρ 0 1 - α t 2

m V = m 0 V 1 - α t 2

Logo, a massa é determinada por:

m = m 0 ( 1 - α t 2 )

Plotando no Excel termos:

Resposta

  1. Q m = 5 k g s
  2. Q = 2 m 3 s
  3. v = 4 m s
  4. m = 25   k g
  5. t = 13,4   s
  6. m f i n a l = 5,1   k g
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Tente uma solução numérica do Problema P3.93 para óleo SAE 30 a 20°C. Seja h = 20c m ,L = 15 c meD = 4m m . Use a aproximação de cisalhamento laminar da Seção 6.4: τ ≈ 8 μ V / D , em que μ é a viscosi
Como uma extensão do Exemplo 3.10, considere a placa e o carrinho (ver Figura 3.10a) desimpedidos horizontalmente, com rodas sem atrito. Deduza (a) a equação do movimento para a velocidade do carrinho
Estenda o problema P3.96 para incluir o atrito na parede devido a uma tensão de cisalhamento média linear (laminar) na forma τ ≈ 8 μ V / D , em que μ é a viscosidade do fluido. Encontre a equação dife
Estenda o Problema P3.90 par ao caso do movimento de um líquido em um tubo U, sem atrito, cuja coluna líquida é deslocada a uma distância Z para cima e então liberada, como na Figura P3.96. Despreze o
Uma certa quantidade de microtubos de diâmetro d e 25 cm de comprimento estão juntos em um tipo de “favo de colmeia”, cuja área transversal total é de 0, 0006 m². A queda de pressão da entrada até à s