Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 10.Exercício - Ex. 3

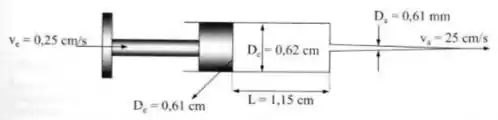
A figura mostra uma seringa para injeções, com as respectivas dimensões. Se a velocidade do êmbolo é 0,25 cm/s e a velocidade do líquido na agulha é 25 cm/s, qual a porcentagem de líquido desperdiçada através da folga entre o êmbolo e o cilindro? (Desprezar o volume contido na agulha)

Passo 1

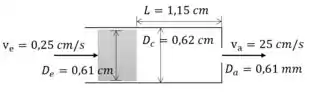
Vamos considerar a seringa como nosso volume de controle e aplicamos a equação da continuidade:

∂ ∂ t ∫ V C ρ d V + ∫ S C ρ ⋅ v → × n → ` ⋅ d A = 0

Como a vazão só é função do tempo, podemos simplificar a derivada parcial

d d t ∫ V C ρ d V + ∫ S C ρ ⋅ v → × n → ` ⋅ d A = 0

Considerando o fluido como incompressível a densidade ρ é constante:

ρ ⋅ d d t ∫ V C d V + ρ ⋅ ∫ S C v → × n → ` ⋅ d A = 0

Resolvendo a integral que representa o volume contido no Volume de Controle:

d d t V + ∫ S C v → × n → ` ⋅ d A = 0

Passo 2

Observe inicialmente a integral: ∫ S C v → × n → ` ⋅ d A . Como podemos solucioná-la?

Perceba que a expressão ∫ S C v → × n → ` ⋅ d A representa a vazão de volumétrica que atravessa a fronteira do sistema. Como nesse sistema não há entrada de fluido, a integral representa a vazão que sai da seringa, seja pela agulha ou pelas folgas.

Em outras palavras:

∫ S C v → × n → ` ⋅ d A = Q f o l g a + Q a

Passo 3

d d t V + ∫ S C v → × n → ` ⋅ d A = 0

Substituindo:

d d t V + Q f o l g a + Q a = 0

Reorganizando:

d d t V = - Q f o l g a + Q a

d V = - Q f o l g a + Q a d t

Integrando ambos os lados, para o lado esquerdo os limites variam entre o volume inicial V i até 0 . Pro lado esquerdo, varia do tempo inicial zero até o tempo final t

∫ V i 0 d V = - ∫ 0 t Q f o l g a + Q a d t

Se considerarmos que as vazões são constantes durante todo o processo:

∫ V i 0 d V = - Q f o l g a + Q a ∫ 0 t d t

Podemos agora resolver as integrais:

- V i = - Q f o l g a + Q a ⋅ t

Ao multiplicarmos a vazão pelo tempo, encontramos o volume perdido:

V i = V f o l g a + Q a ⋅ t

Agora é isolarmos a volume perdido na folga:

V f o l g a = V i - Q a t

Pronto, temos uma equação que nos fornecerá o volume perdido na folga. Mas pra isso precisamos saber: Qual o volume inicial? Qual é a vazão que saí pela agulha? Quanto tempo dura este processo?

Passo 4

O volume inicial é fácil de calcular. Basta calcular o volume da seringa, utilizando o comprimento da seringa e o seu diâmetro.

V i = V s e r i n g a

V i = π D c 2 4 ⋅ L

V i = 1 4 ⋅ π ⋅ 0,62   c m 2 ⋅ 1,15   c m

V i = 0,110515 π   c m 3

Para calcular a vazão que sai pela agulha basta utilizar a velocidade de saída e o diâmetro da agulha:

Q a = A a ⋅ v a

Q a = π D a 2 4 ⋅ v a

Q a = π 0,61   m m 2 4 ⋅ 25 c m s

Q a = π 0,061   c m 2 4 ⋅ 25 c m s

Q a = 0,02325625 π c m 3 s

E o tempo também é fácil de descobrir. Basta calcular o tempo que o embolo leva pra atravessar todo o percurso L da seringa!

t = L v e

t = 1,15   c m 0,25 c m s

t = 1,15   c m 0,25 c m s

t = 4,6   s

Passo 5

Agora é só aplicar os valores:

V f o l g a = V i - Q a t

V f o l g a = 0,110515 π   c m 3 - 0,02325625 π c m 3 s ⋅ 4,6   s

V f o l g a = 0,00353625 π   c m 3

E agora calculamos a porcentagem que representa:

V f o l g a V i = 0 , 00353625 π   0,110515 π  

V f o l g a V i = 0,032

V f o l g a V i = 3,2 %

Resposta

V f o l g a V i = 3,2 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

De acordo com o teorema de Torricelli, a velocidade de um fluido escoando por um orifício em um tanque é V ≈ 2 g h 1 2 , em que h é a altura da água acima do orifício. Considere que o orifício tenha u
Um motor de foguete opera em regime permanente como mostra a figura abaixo. Os produtos da combustão que escoam através do bocal de descarga aproximam-se de um gás perfeito com peso molecular de 28. P
Água a 20°C escoa em regime permanente através a bifurcação de tubulação mostrada na figura a seguir, entrando na seção 1 com 76 L/min. A velocidade média na seção 2 é de 2,5 m/s. Uma porção do escoam
Em contraste com o foguete de combustível líquido da questão anterior, o foguete com propelente sólido abaixo é autocontido e não possui dutos de entrada. Aplicando uma análise de volume de controle p
Um cilindro sólido de aço de 4,5 cm de diâmetro e 12 cm de comprimento, com massa de 1500g, cai concentricamente por uma cuba vertical de 5 cm de diâmetro cheia de óleo (d = 0,89). Considerando o óleo