Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 76

O revestimento sobre uma superfície metálica com dimensões de 1 m por 2m é curado pela sua colocação sob uma superfície eletricamente aquecida de dimensões equivalentes, a uma distância de 0,5 m. O conjunto é exposto a uma grande vizinhança a 300 K. O aquecedor encontra-se isolado termicamente no seu lado superior e está alinhado com a superfície

revestida. A superfície aquecida e a superfície revestida podem ser aproximadas por corpos negros. Durante o procedimento de cura, as superfícies aquecida e revestida são mantidas a 700 e 400 K, respectivamente. Os efeitos convectivos podem ser desprezados.

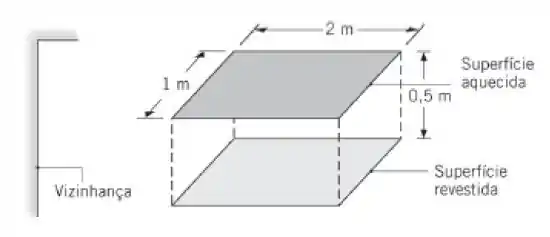
  1. Qual é a potência elétrica, qele, exigida para operar o aquecedor?

  2. Qual será o valor de qele se as superfícies forem conectadas por paredes laterais rerradiantes?

Passo 1

Vamos lá!!!

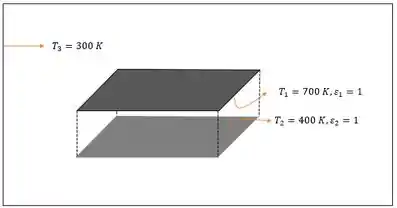
q e l t = q 1 = A 1 F 12 σ T 1 4 - T 2 4 + A 1 F 13 σ ( T 1 4 - T 3 4 )

Para achar F 12 vamos usar a figura 13.4 :

Y L = 1 0,5 = 2 ; X L = 2 0,5 = 4

Achamos F 12 ≈ 0,5 , pela regra da soma:

F 13 = 1 - 0,5 = 0,5

Sabendo que σ = 5,67 × 10 - 8   W / m 2 K 4 , podemos substituir:

q e l t = 2 × 0,5 × 5,67 × 10 - 8 700 4 - 400 4 + 2 × 0,5 × 5,67 × 10 - 8 700 4 - 300 4

Calculando:

q e l e = 25,316   W

Passo 2

Agora a gente vai colocar paredes isoladas entre a superfície 1 e 2 , assim, para calcular q 1 usamos:

q 1 = σ ( T 1 4 - T 2 4 ) 1 - ε 1 ε 1 A 1 + 1 A 1 F 12 + 1 A 1 F 1 R + 1 A 2 F 2 R - 1 + 1 - ε 2 ε 2 A 2

Mas, ε 1 = ε 2 = 1 e A 1 = A 2 , logo podemos fazer:

q 1 = A 1 σ ( T 1 4 - T 2 4 ) 1 F 12 + 1 F 1 R + 1 F 2 R - 1

Agora é só substituir:

q 1 = 2 × 5,67 × 10 - 8 × ( 700 4 - 400 4 ) 1 0,5 + 1 0,5 + 1 0,5 - 1

Calculando:

q 1 = q e l e = 18,243   W

Uhuuuul!!

Resposta

  1. q e l e = 25,316   W
  2. q e l e = 18,243   W
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um coletor solar é formado por um longo duto através do qual ar é soprado; sua seção transversal forma um triângulo equilátero com 1 m de lado. Um dos lados é uma cobertura de vidro com emissividade ε
Uma parede composta é feita com duas grandes placas separadas por folhas de isolamento refratário, como mostrado na figura. No processo de instalação, as folhas de espessura L = 50 mm e condutividade
Um forno elétrico com duas seções de aquecimento, superior e inferior, é usado para tratar termicamente um revestimento que é aplicado em ambas as superfícies de uma placa metálica que é inserida na m
Um pequeno disco com diâmetro D1 = 50 mm e emissividade ε1 = 0,6 é mantido a uma temperatura de T1 = 900 K. O disco é coberto com uma barreira de radiação hemisférica com o mesmo diâmetro e uma emissi
Considere uma cavidade cilíndrica de diâmetro D = 100 mm e profundidade L = 50 mm, cujas parede lateral e fundo são difusas e cinzas com uma emissividade de 0,6 e estão a uma temperatura uniforme de 1