Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 45

O rotor de um ventilador centrífugo tem raio de 15 cm e lâmina com largura de 6,1 cm na entrada, e um raio de 30 cm e uma lâmina com largura de 3,4 cm na saída. O ventilador fornece ar atmosférico a 20°C e 95 kPa. Desprezando as perdas e considerando que as componentes tangenciais da velocidade do ar na entrada e saída sejam iguais à velocidade do rotor nas respectivas localizações, determine a vazão em volume quando a velocidade rotacional do eixo é de 800 rpm e o consumo de energia do ventilador é de 120 W. Determine também as componentes normais da velocidade na entrada e na saída do rotor.

Passo 1

Pra começar, vamos fazer um esqueminha do ventilador centrifugo!!!

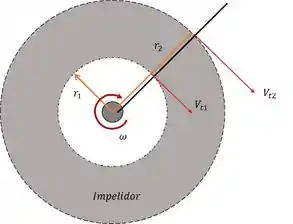
O torque no eixo pode ser dado por:

T e i x o = m ˙ ( r 2 V t 2 - r 1 V t 1 )

No caso das velocidades tangenciais serem iguais as velocidades do rotor, temos:

V t 1 = ω r 1

V t 2 = ω r 2

A vazão mássica na fórmula do torque pode ser substituida por:

m ˙ = ρ V ˙

Substituindo essas informações:

T e i x o = ρ V ˙ ω ( r 2   2 - r 1     2 )

A velocidade angular ω é dada por:

ω = 2 π n ˙

E W ˙ pode ser calculado usando a seguinte expressão:

W ˙ = ω T e i x o

Substituindo:

W ˙ = ρ V ˙ ω 2 ( r 2   2 - r 1     2 )

Agora a gente pode dar uma arrumadinha e...

V ˙ = W ˙   ρ ω 2 r 2   2 - r 1     2  

Assim achamos a vazão volumétrica que o enunciado ta pedindo!!

Ahhh, não temos ρ , mas calminha porque podemos achar ele usando a lei dos gases ideiais!

ρ = P R T

Agora vamos ver como a gente acha as componentes normais de velocidade!

V t 1 = V ˙ 2 π r 1 b 1

V t 2 = V ˙ 2 π r 2 b 2

Aqui b 1 e b 2 são as larguras dadas no enunciado!

Agora podemos colocar a mão na massa!!!

Passo 2

Primeiro vamos achar o ρ :

ρ = 95   k P a 0,287 k P a k g ∙ K × ( 293   K ) = 1,130   k g / m 3

A velocidade angular ω :

ω = 2 π × 800   r p m × 1   m i n 60   s = 83,78   r a d / s

Agora temos tudo pra usar essa expressão aqui:

V ˙ = W ˙   ρ ω 2 r 2   2 - r 1     2  

Substituindo os valores do enunciado:

V ˙ = 120   1000 × 83,78 2 0,30 2 - 0,15 2 = 0,224 m 3 s

Tcharaaam! Temos a vazão volumétrica, agora só falta calcular a vazão mássica!

Passo 3

Substituindo os valores:

V t 1 = 0,224 2 π ( 0,15 ) ( 0,061 ) = 3,90 m s

V t 2 = 0,224 2 π ( 0,30 ) ( 0,034 ) = 3,40   m / s

Achamos!!

Resposta

A vazão volumétrica é:

V ˙ = 0,224 m 3 s

As componentes normais da velocidade na entrada e na saída do rotor:

V t 1 = 0,224 2 π ( 0,15 ) ( 0,061 ) = 3,90 m s

V t 2 = 0,224 2 π ( 0,30 ) ( 0,034 ) = 3,40   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tanque móvel mostrado deve ser desacelerado pelo abaixamento de uma concha que capta água de um reservatório. A massa e a velocidade iniciais do tanque, com seu conteúdo, são m 0 e u 0 , respectivam
Deseja-se uma bomba que, acoplada a um motor de 3450 rpm, produza uma altura manométrica teórica de 80 m. O ângulo de entrada das pás deve ser de 15º e o de saída, de 30º. Sendo d 1 = 10c m , quanto d
Uma bomba centrífuga tem pás com ângulo de entrada 15º e de saída de 25º. A rotação é 1720 rpm e os diâmetros de entrada e saída são, respectivamente, de 10cm e 25cm. Sendo v u 1 = 0 e v r 1 = v r 2 ,
No dispositivo da figura, o pistão de peso G = 29,4k N desce muito lentamente dentro do cilindro de área 2m 2 , empurrando a água ( γ = 10 4N / m 3 ) pelos dois cotovelos instalados simetricamente. A
O tampão de base circular da figura está colocado concentricamente na tubulação horizontal de seção circular para controlar a vazão de água. Sendo ρ = 1000k g / m 3 e desprezando a perda de carga, det