Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 3.Problemas - Ex. 76
76 – Difusão em condições de estado estacionário e unidimensional existe dentro do cilindro composto mostrado. Os três materiais possuem condutividades térmicas de kA, kB=2kA, kC=kA, respectivamente. Uma geração volumétrica uniforme de energia, , ocorre dentro do material B, havendo resistência a condução de rA até rB. O cilindro é colocado dentro de uma câmara de vácuo, na qual somente perda por radiação ocorre em r=rC.
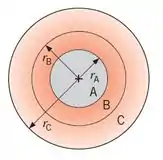
(A) Escreva a forma apropriada da equação do calor para cada um dos três materiais.
(B) Escreva uma expressão para a temperatura T(rC) em termos das variáveis relevantes fornecidas acima, a temperatura da vizinhança TViz, e a emissividade da superfície exposta.
Passo 1
Você pode iniciar estabelecendo as considerações:
-propriedades constantes;
-estado estacionário;
-condução unidimensional;
-geração de energia na forma de calor uniforme;
-resistência a condução apenas no material B;
-a superfície externa do material C está sujeita a radiação.
Passo 2
Pelo balanço de energia em termos do balanço de energia térmica:
Onde,
-qcond é taxa de transferência de calor por condução;
-qconv é a taxa de transferência de calor por convecção;
-qrad é a taxa de transferência de calor por radiação;
-qg é a taxa de geração de calor;
A Eq1 será a eq. base para modelarmos as eq’s do calor para cada material.
Passo 3
(A)
Material A:
Nesse material, não há geração de energia térmica, e também não tem fluido em contato e nem há efeitos de calor por radiação, assim
Como não há resistência entre de rA até r0 (centro):
Pela Lei de Fourier
Onde,
Passo 4
Material B:
Nesse material, há geração de energia volumétrica de forma uniforme, e também não tem fluido em contato e nem há efeitos de calor por radiação, e há existência de resistência ao transporte de calor entre rA e rB, assim
Como há resistência entre de rA até rB:
Onde,
Como
Passo 5
Material C:
Nesse material, não há geração de energia térmica, e também não tem fluido em contato, mas tem efeitos de calor por radiação, assim
Como não há resistência entre de rA até r0 (centro):
Pela Lei de Fourier
Como
Onde,
Pela equação da transferência de calor por radiação
Onde,
-ε é a emissividade do meio;
-σ é a constante de Stefan-Boltzmann, σ=5,67x10-8 W/m2.K4;
-TViz é a temperatura da vizinhança;
-L é o comprimento do cilindro.
Assim,
Passo 6
(B)
Distribuição de T:
Como se trata de um cilindro, então pela Eq. Global do calor para um cilindro, em coordenadas cilíndricas (r, θ, z):
Onde,
-r é a coordenada radial;
-θ é a coordenada angular;
-z é a coordenada axial;
-, é geração volumétrica de energia;
-T é a temperatura;
-k é a condutividade térmica;
-cp é o calor especifico;
-ρ é a densidade;
-t é o tempo;
Como se trata de estado estacionário, então
Pela transferência de calor unidimensional (transferência de calor na direção radial, r)
E com geração volumétrica de energia, assim a eq. global da transferência de calor é simplificada para:
Passo 7
Esta equação é uma equação diferencial (ED), vamos usar uma técnica então para resolve-la chamada separação de variáveis
Resolvendo por separação de variáveis:
Integrando em relação a r
Integrando novamente em relação a r
Passo 8
Aplicando as condições de contorno:
Vamos achar que:
Portanto,
Essa é a expressão da distribuição de temperatura em função do raio
Passo 9
Para determinarmos T(rC), vamos aplicar um balanço de energia global no sistema:
Pela Eq1:
Como analise global, não temos convecção (pois não tem fluido em contato com os materiais) e nem condução de calor (só temos condução de calor no interior dos materiais), assim
Pela expressão da radiação
E encontramos também que:
Isolando o termo da geração de energia:
Onde,
-VB é o volume do cilindro B;
O volume do cilindro B é dado por:
Assim,
Isolando TC:
Resposta
A)
B)