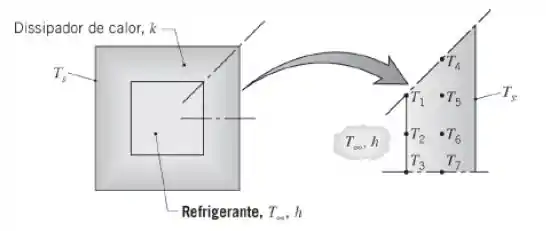
Seja um dissipador de calor de alumínio , como o mostrado esquematicamente no Problema 4.28. As larguras interna e externa do canal quadrado são w = 20 mm e W = 40 mm, respectivamente, e uma temperatura na superfície externa de é mantida pela série de chips eletrônicos. Nesse caso, não se conhece a temperatura da superfície interna, mas sim as condições associadas ao escoamento do refrigerante através do canal. Desejamos determinar a taxa de transferência de calor para o refrigerante por unidade de comprimento do canal. Com esse propósito, considere uma seção simétrica do canal e uma malha bidimensional com Δx = Δy = 5 mm.
- Para e , determine as temperaturas desconhecidas, , e a taxa de transferência de calor por unidade de comprimento do canal, q′.
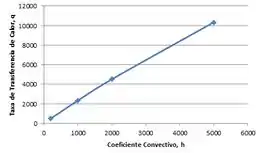
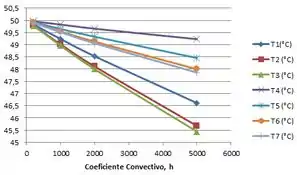
- Avalie o efeito de variações no h nas temperaturas desconhecidas e na taxa de transferência de calor.
Passo 1
Mais uma bem legal ein galerinha !!
Aqui nós precisamos desenhar para conseguir ver melhor o que vai rolar !!
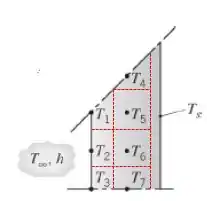
Começando pelo nó 2, nós vamos observar condução vindo dos nós 2 e 5 e convecção do fluido interno, certo?
Aplicando o balanço de energia:
Vamos relembrar como são calculados cada um deles?
Colocando no balanço:
Como :
Substituindo:
Como o ponto 2 e 3 são pontos nodais em uma superfície plana com convecção:
Substituindo:
Se achamos no ponto 2, agora é só fazermos igual no ponto 3:
Substituindo nós obtemos:
Passo 2
Aqui nós não temos convecção, somente condução vindo do espaço próximo à temperatura e do ponto 5:
Substituindo nós obtemos:
Agora nós vamos analisar o que está acontecendo nos pontos 5, 6 e 7, ok?
Como todos são pontos nodais no interior:
Resolvendo as equações
Passo 3
Para o fluxo de calor total nós precisamos lembrar que na superfície cuja a transferência por convecção ocorre estão os pontos 1, 2 e 3. Então a taxa de transferência de calor da superfície será a soma das taxas de calor por convecção para cada um deles:
Como nós temos 8 partes iguais ao longo da figura:
Substituindo nossos dados:
Acabamos a letra (a) e vamos seguindo rapidinho pra (b) ein !!
Passo 4
Na letra (b) nós queremos avaliar o efeito de variações no h nas temperaturas desconhecidas e na taxa de transferência de calor, certo?
Se variamos o h então é só nós fazermos tudo que fizemos nos Passos 1, 2 e 3 e obtemos os novos valores.
Para as temperaturas:
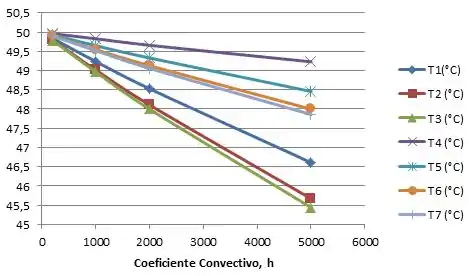
E fazendo um especial para a troca de calor:
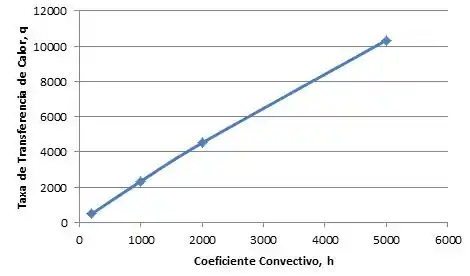
Tranquilinha, não é?
Resposta
;