Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 52

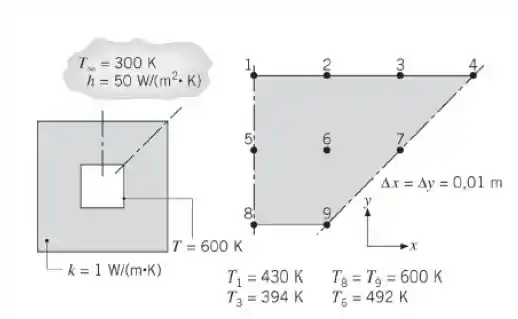
Seja o canal quadrado mostrado na figura, operando sob condições de regime estacionário. A superfície interna do canal está a uma temperatura uniforme de 600 K, enquanto a superfície externa está exposta à troca de calor por convecção com um fluido a 300 K e um coeficiente convectivo de 50 W m 2 K . Com base em um elemento simétrico do canal, foi construída uma malha bidimensional e identificados os seus nós. As temperaturas nos nós 1, 3, 6, 8 e 9 são fornecidas.

  1. Partindo de volumes de controle apropriadamente definidos, deduza as equações de diferenças finitas para os nós 2, 4 e 7, e determine as temperaturas T 2 ,   T 4 e T 7 ( K ) .
  2. Calcule a perda de calor por unidade de comprimento do canal.

Passo 1

Mais uma bem legal ein galerinha !!

Aqui nós precisamos desenhar para conseguir ver melhor o que vai rolar !!

Começando pelo nó 2, nós vamos pegar um volume diferencial e ver que nós temos q ' a , como calor de convecção ao qual o nó está exposto, q ' b , q ' c   e   q ' d como calores de condução devido aos pontos laterais, ok?

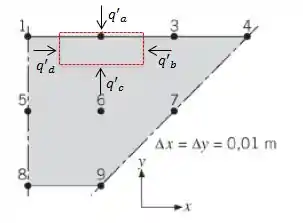
Aplicando o balanço de energia:

q ' a + q ' b + q ' c + q ' d = 0

Vamos relembrar como são calculados cada um deles?

q ' a = h ∆ x T ∞ - T 2

q ' b = k ∆ y 2 T 3 - T 2 ∆ x  

q ' c = k ∆ x T 6 - T 2 ∆ y

q ' d = k ∆ y 2 T 1 - T 2 ∆ x

Colocando no balanço:

h ∆ x T ∞ - T 2 + k ∆ y 2 T 3 - T 2 ∆ x + k ∆ x T 6 - T 2 ∆ y + k ∆ y 2 T 1 - T 2 ∆ x = 0

2 h ∆ x T ∞ - T 2 + k ∆ y T 3 - T 2 ∆ x + 2 k ∆ x T 6 - T 2 ∆ y + k ∆ y T 1 - T 2 ∆ x = 0

2 h ∆ x T ∞ - 2 h ∆ x T 2 + k ∆ y ∆ x T 3 - k ∆ y ∆ x T 2 + 2 k ∆ x ∆ y T 6 - 2 k ∆ x ∆ y T 2 + k ∆ y ∆ x T 1 - k ∆ y ∆ x T 2 = 0

2 h ∆ x T ∞ - 2 h ∆ x T 2 + k ∆ y ∆ x T 3 - 2 k ∆ y ∆ x T 2 + 2 k ∆ x ∆ y T 6 - 2 k ∆ x ∆ y T 2 + k ∆ y ∆ x T 1 = 0

Isolando T 2 :

T 2 2 h ∆ x + 2 k ∆ y ∆ x + 2 k ∆ x ∆ y = 2 h ∆ x T ∞ + k ∆ y ∆ x T 3 + 2 k ∆ x ∆ y T 6 + k ∆ y ∆ x T 1

Como ∆ x = ∆ y :

T 2 2 h ∆ x + 2 k + 2 k = 2 h ∆ x T ∞ + k T 3 + 2 k T 6 + k T 1

T 2 2 h ∆ x + 4 k = 2 h ∆ x T ∞ + k T 3 + 2 k T 6 + k T 1

T 2 = 2 h ∆ x T ∞ + k T 3 + 2 k T 6 + k T 1 2 h ∆ x + 4 k

Sabendo que:

k = 1 W m K

h = 50 W m 2 K

∆ x = 0,01   m

T 1 = 430   K

T 3 = 394   K

T 6 = 492   K

T ∞ = 300   K

Colocando na fórmula:

T 2 = 2 50 W m 2 K 0,01   m 300   K + 1 W m K 394   K + 2 1 W m K 492   K + 1 W m K 430   K 2 50 W m 2 K 0,01   m + 4 1 W m K

T 2 = 421,6   K

Passo 2

Agora nós faremos a mesma coisa, mas para o nó 4, olhando o volume diferencial:

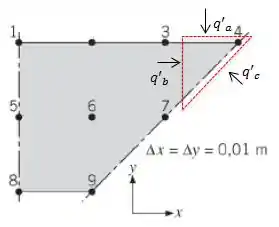
Aplicando o balanço de energia:

q ' a + q ' b + q ' c = 0

Vamos relembrar como são calculados cada um deles?

q ' a = h ∆ x 2 T ∞ - T 4

q ' b = k ∆ y 2 T 3 - T 4 ∆ x  

Como q ' c está num ponto adiabático:

q ' c = 0

Colocando no balanço:

h ∆ x 2 T ∞ - T 4 + k ∆ y 2 T 3 - T 4 ∆ x + 0 = 0

h ∆ x T ∞ - h ∆ x T 4 + k ∆ y ∆ x T 3 - k ∆ y ∆ x T 4 = 0

Isolando T 4 :

T 4 h ∆ x + k ∆ y ∆ x = h ∆ x T ∞ + k ∆ y ∆ x T 3

Como ∆ x = ∆ y :

T 4 h ∆ x + k = h ∆ x T ∞ + k T 3

T 4 = h ∆ x T ∞ + k T 3 h ∆ x + k

Colocando na fórmula:

T 4 = 50 W m 2 K 0,01   m 300   K + 1 W m K 394   K 50 W m 2 K 0,01   m + 1 W m K

T 4 = 362,7   K

Então só nos falta o nó 7, certo?

O ponto está na diagonal que é simétrica e adiabática, então nós podemos calcular a sua temperatura usando os dados da Tabela 4.2:

T 7 = 1 4 T 3 + T 3 + T 6 + T 6

Não se esqueçam que tiramos isso da simetria !!

T 7 = 1 2 T 3 + T 6

Substituindo:

T 7 = 1 2 394   K + 492   K

T 7 = 443   K

E com isso nós finalizamos a letra (a) !!

Passo 3

Na letra (b) nós queremos calcular a perda de calor por unidade de comprimento do canal, não é?

O calor é perdido por convecção na superfície, sendo assim cada nó 1, 2, 3 e 4 perderam uma certa quantidade de calor:

q ' t o t a l = q ' 1 + q ' 2 + q ' 3 + q ' 4

Sabemos que:

q ' 1 = h ∆ x 2 T 1 - T ∞

q ' 2 = h ∆ x T 2 - T ∞

q ' 3 = h ∆ x T 3 - T ∞

q ' 4 = h ∆ x 2 T 4 - T ∞

Substituindo:

q ' t o t a l = h ∆ x 2 T 1 - T ∞ + h ∆ x T 2 - T ∞ + h ∆ x T 3 - T ∞ + h ∆ x 2 T 4 - T ∞

Colocando nossos dados:

q ' t o t a l = 50 W m 2 K 0,01   m 2 430   K - 300   K + 50 W m 2 K 0,01   m 421,6   K - 300   K + 50 W m 2 K 0,01   m 394 K - 300   K + 50 W m 2 K 0,01   m x 2 362,7   K - 300   K

q ' t o t a l = 156 W m

Tranquilinha, não é?

Resposta

  1. T 2 = 421,6   K           T 4 = 362,7   K         T 7 = 443   K ;
  2. q ' t o t a l = 156 W m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um dos pontos fortes dos métodos numéricos é a sua capacidade de lidar com condições de contorno complexas. No esboço, a condição de contorno muda de fluxo térmico especificado, q s ' ' (para dentro d
As superfícies superior e inferior de uma barra de condução são resfriadas por convecção com ar a T ∞ , com h s ≠ h i . As laterais são resfriadas pela manutenção de contato com sumidouro de calor a T
Seja a malha bidimensional ( ∆ x = ∆ y ) representando condições de regime estacionário, sem geração volumétrica interna de calor, em um sistema com condutividade térmica k . Um dos contornos é mantid
Determine as expressões para q ( m - 1 , n ) → ( m , n ) ,q m + 1 , n → ( m , n ) ,q m ,n + 1 → ( m , n ) e q m ,n - 1 → ( m , n ) , na condução associada a um volume de controle que abrange dois dife
Deduza as equações de diferenças finitas nodais para as seguintes considerações.(a) Nó (m,n) sobre um contorno diagonal sujeito à convecção com um fluido a uma temperatura T ∞ , com um coeficiente de