Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 57

Temperaturas em regime estacionário em pontos nodais escolhidos da seção simétrica de um canal de escoamento são conhecidas: T 2 = 95,47 ° C ,     T 3 = 117,3 ° C ,     T 5 =   79,79 ° C ,     T 6 =   77,29 ° C ,     T 8 =   87,28 ° C   e   T 10 =   77,65 ° C . Há na parede geração de calor volumétrica e uniforme de q ˙ =   10 6 W m 3 e a sua condutividade térmica é igual a k   =   10 W m K . Há convecção nas superfícies interna e externa do canal com fluidos com temperaturas T ∞ , i = 50 ° C e T ∞ , e =   25 ° C , com coeficientes convectivos de h i = 500 W m 2 K e h e = 250 W m 2 K .

  1. Determine as temperaturas nos pontos nodais 1, 4, 7 e 9.
  2. Calcule a taxa de transferência de calor por unidade de comprimento W m da superfície externa A para o fluido adjacente.
  3. Calcule a taxa de transferência de calor por unidade de comprimento do fluido interno para a superfície B.
  4. Verifique se os seus resultados estão consistentes com um balanço de energia global na seção do canal.

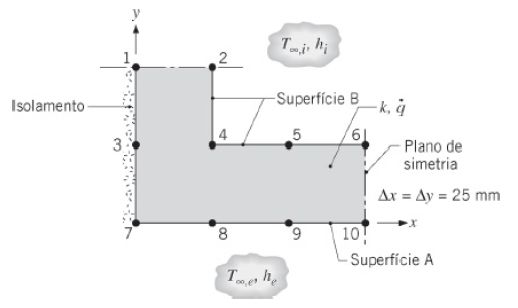
Passo 1

Boom galerinha, na letra (a) nós queremos achar as temperaturas nos pontos nodais 1, 4, 7 e 9, certo?

Para isso vamos fazer a análise para cada ponto, ok?

Começando pelo ponto 1:

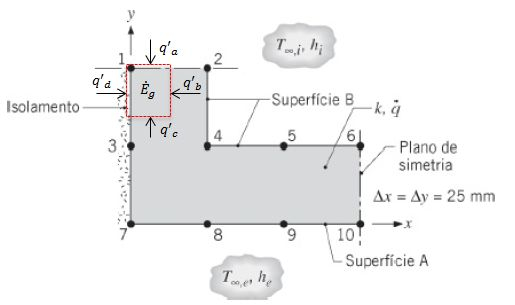
Quando fazemos o balanço de energia:

q ' a + q ' b + q ' c + q ' d + E g ˙ = 0

Sabemos que:

q ' a = q ' d = 0  

Isso porque q ' d é relativo ao lado isolado e q ' a é referente ao calor do restante do tubo, como não temos outras informações sobre as temperaturas, assumimos o valor zero, ok?

q ' b = k ∆ y 2 T 2 - T 1 ∆ x  

q ' c = k ∆ x 2 T 3 - T 1 ∆ y

E g ˙ = q ˙ ∆ x 2 ∆ y 2

Então:

k ∆ y 2 T 2 - T 1 ∆ x + k ∆ x 2 T 3 - T 1 ∆ y + q ˙ ∆ x ∆ y 4

Como ∆ x = ∆ y :

k 2 T 2 - T 1 + k 2 T 3 - T 1 + q ˙ ∆ x 2 4 = 0

Isolando T 1 :

T 1 = T 2 + T 3 2 + q ˙ ∆ x 2 4 k

Substituindo nossos dados:

T 1 = 95,47 ° C + 117,3 ° C 2 + 10 6 W m 3 0,025   m 2 4 10 W m k

T 1 = 122   ° C

Para o nó 4:

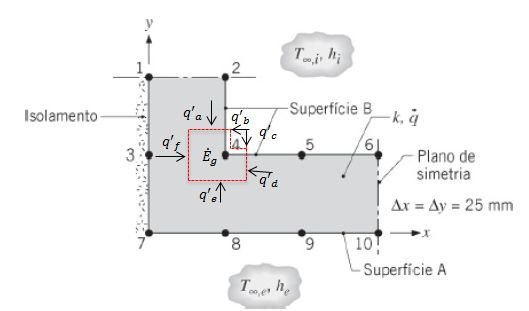
Quando fazemos o balanço de energia:

q ' a + q ' b + q ' c + q ' d + q ' e + q ' f + E g ˙ = 0

Sabemos que:

q ' a = k ∆ x 2 T 2 - T 4 ∆ y  

q ' b = h i ∆ y 2 T ∞ , i - T 4

q ' c = h i ∆ x 2 T ∞ , i - T 4

q ' d = k ∆ y 2 T 5 - T 4 ∆ x

q ' e = k ∆ x T 8 - T 4 ∆ x

q ' f = k ∆ y T 3 - T 4 ∆ x

E g ˙ = q ˙ 3 ∆ x 2 ∆ y 2

Então:

k ∆ x 2 T 2 - T 4 ∆ y + h i ∆ y 2 T ∞ , i - T 4 + h i ∆ x 2 T ∞ , i - T 4 + k ∆ y 2 T 5 - T 4 ∆ x + k ∆ x T 8 - T 4 ∆ x + k ∆ y T 3 - T 4 ∆ x + q ˙ 3 ∆ x 2 ∆ y 2 = 0

Como ∆ x = ∆ y :

k 2 T 2 - T 4 + h i ∆ y 2 T ∞ , i - T 4 + h i ∆ x 2 T ∞ , i - T 4 + k 2 T 5 - T 4 + k T 8 - T 4 + k T 3 - T 4 + 3 q ˙ ∆ x 2 4 = 0

Isolando T 4 :

T 4 = T 2 + 2 T 3 + T 5 + 2 T 8 + 2 h i ∆ x k T ∞ , i + 3 q ˙ ∆ x 2 2 k 6 + 2 h i ∆ x k

Substituindo nossos dados:

T 4 = 95,47 ° C + 2 117,3 ° C + 79,79 ° C + 2 87,28 ° C   + 2 500 W m 2 K 0,025   m 10 W m k 50 ° C + 3 × 10 6 W m 3 0,025   m 2 2 10 W m k 6 + 2 500 W m 2 K × 0,025   m 10 W m k

T 4 = 94,5   ° C

Passo 2

Para o nó 7:

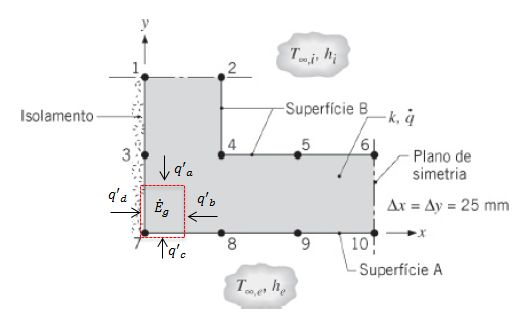
Quando fazemos o balanço de energia:

q ' a + q ' b + q ' c + q ' d + E g ˙ = 0

Sabemos que:

q ' a = k ∆ x 2 T 3 - T 2 ∆ y  

q ' b = k ∆ y 2 T 8 - T 7 ∆ x

q ' b = h 0 ∆ x 2 T ∞ , 0 - T 7

q ' d = 0  

E g ˙ = q ˙ ∆ x ∆ y 4

Então:

k ∆ x 2 T 3 - T 2 ∆ y + k ∆ y 2 T 8 - T 7 ∆ x + h 0 ∆ x 2 T ∞ , 0 - T 7 + q ˙ ∆ x ∆ y 4 = 0

Como ∆ x = ∆ y :

k 2 T 3 - T 2 + k 2 T 8 - T 7 + h 0 ∆ x 2 T ∞ , 0 - T 7 + q ˙ ∆ x ∆ y 4 = 0

Isolando T 7 :

T 7 = T 3 + T 8 + h 0 ∆ x k T ∞ , 0 + q ˙ ∆ x 2 2 k 2 + h 0 ∆ x k

Substituindo nossos dados:

T 7 = 117,3 ° C + 87,28 ° C   + 2 50 W m 2 K 0,025   m 10 W m k 2 5 ° C + 10 6 W m 3 0,025   m 2 2 10 W m k 2 + 250 W m 2 K 0,025   m 10 W m k

T 7 = 95,8 ° C

Para o nó 9:

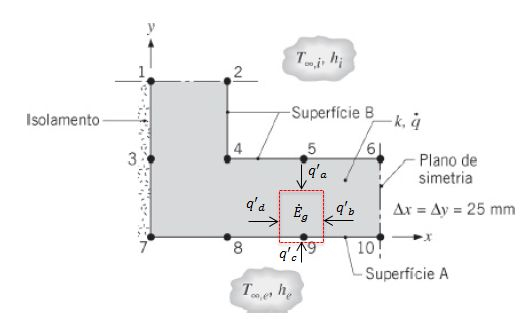
Quando fazemos o balanço de energia:

q ' a + q ' b + q ' c + q ' d + E g ˙ = 0

Sabemos que:

q ' a = k ∆ x T 5 - T 9 ∆ y  

q ' b = k ∆ y 2 T 10 - T 9 ∆ x

q ' c = h 0 ∆ x T ∞ , 0 - T 9

q ' d = k ∆ y 2 T 8 - T 9 ∆ x  

E g ˙ = q ˙ ∆ x ∆ y 2

Então:

k ∆ x T 5 - T 9 ∆ y + k ∆ y 2 T 10 - T 9 ∆ x + h 0 ∆ x T ∞ , 0 - T 9 + k ∆ y 2 T 8 - T 9 ∆ x + q ˙ ∆ x ∆ y 2 = 0

Como ∆ x = ∆ y :

k T 5 - T 9 + k 2 T 10 - T 9 + h 0 ∆ x T ∞ , 0 - T 9 + k 2 T 8 - T 9 + q ˙ ∆ x 2 2 = 0

Isolando T 9 :

T 9 = T 5 + 0,5 T 8 + 0,5 T 10 + h 0 ∆ x k T ∞ , 0 + q ˙ ∆ x 2 2 k 2 + h 0 ∆ x k

Substituindo nossos dados:

T 9 = 79,79 ° C + 0,5 ( 87,28 ° C ) + 0,5 ( 77,65 ° C )   + 250 W m 2 K 0,025   m 10 W m k 25 ° C + 10 6 W m 3 0,025   m 2 2 10 W m k 2 + 250 W m 2 K 0,025   m 10 W m k

T 9 = 79,67 ° C

Acabamos a letra (a), mas não se animem porque ainda não acabamos !!

Passo 3

Agora, na letra (b) nós queremos achar a taxa de transferência de calor por unidade de comprimento W m da superfície externa A para o fluido adjacente.

Na superfície A nós temos os pontos 7, 8, 9 e 10. Então a taxa de transferência de calor da superfície A será a soma das taxas de calor por convecção para cada um deles:

q ' A = h 0 ∆ x 2 T 7 - T ∞ , 0 + ∆ x T 8 - T ∞ , 0 + ∆ x T 9 - T ∞ , 0 + ∆ x 2 T 10 - T ∞ , 0

Substituindo nossos dados:

q ' A = 250 W m K 0,025   m 2 95,8 ° C - 25 ° C + 0,025   m 87,28 ° C - 25 ° C + 0,025   m 79,67 ° C - 25 ° C + 0,025   m 2 77,65 ° C - 25 ° C

q ' A = 1117 W m

Passo 4

Agora, na letra (c) nós queremos achar a taxa de transferência de calor por unidade de comprimento W m da superfície externa B para o fluido adjacente.

Na superfície A nós temos os pontos 2, 4, 5 e 6. Então a taxa de transferência de calor da superfície B será a soma das taxas de calor por convecção para cada um deles:

q ' B = h i ∆ y 2 T ∞ , i - T 2 + ∆ y 2 + ∆ x 2 T ∞ , i - T 4 + ∆ x T ∞ , i - T 5 + ∆ x 2 T ∞ , i - T 6

Substituindo nossos dados:

q ' B = 5 0 0 W m K 0,025   m 2 50 ° C - 95,47 ° C + 0,025   m 2 + 0,025   m 2 50 ° C - 94,5 ° C + 0,025   m 50 ° C - 79,79 ° C + 0,025   m 2 50 ° C - 77,29 ° C

q ' B = - 1383 W m

Passo 5

Na letra (d) nós precisamos confirmar se os seus resultados estão consistentes com um balanço de energia global na seção do canal!!

Se usarmos o balanço de energia:

E ˙ e n t r a + E ˙ g e r a d a - E ˙ s a i = 0

Substituindo:

- q ' A + q ' B + E ˙ g e r a d a = 0

Colocando os nossos valores:

- 1117 W m - 1383 W m + E ˙ g e r a d a = 0

E ˙ g e r a d a = 2500 W m

Se lembrarmos que:

E ˙ g e r a d a = q ˙ A = 10 6 W m 3 0,025   × 0,05 + 0,025   × 0,05   m 2

E ˙ g e r a d a = 2500 W m

O mesmo valor, não é?

Isso comprova os nossos resultados !!

Resposta

  1. T 1 = 122   ° C     T 4 = 94,5   ° C       T 7 = 95,8 ° C     |     T 9 = 79,67 ° C ;
  2. q ' A = 1117 W m ;
  3. q ' B = - 1383 W m ;
  4. C o m o   v i s t o   a c i m a ‼
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma configuração cilíndrica bidimensional, os espaçamentos radiais ( ∆ r ) e angulares ( ∆ φ ) entre os pontos nodais são uniformes. O contorno em r = r , está em uma temperatura uniforme T i . Na
Materiais funcionalmente graduados são intencionalmente fabricados para estabelecerem uma distribuição espacial de propriedades no produto final. Seja um objeto L × L bidimensional, com L = 20 mm. A d
Um canal por onde passam gases quentes de exaustão apresenta uma seção transversal quadrada de 300 mm de lado. As paredes são construídas com tijolos refratários com 150 mm de espessura e condutividad
Uma longa barra condutora com seção transversal retangular ( 20m m×30m m ) e condutividade térmica k=20 W m K , experimenta geração térmica uniforme a uma taxa de q ˙ =5×10 7 W m 3 , enquanto suas sup
As temperaturas (em K), em regime estacionário, de três pontos nodais de uma longa barra retangular são fornecidas na figura. A barra experimenta uma taxa de geração volumétrica de calor uniforme igua