Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 6º - Capítulo 5.Problemas - Ex. 127
Sejam o módulo de condução térmica e as condições de operação do Problema 4.76. Para calcular a resposta transiente da placa fria, que possui uma difusividade térmica cr = 75 X 10-6
trrVs, considere que, quando o módulo é ativado em t — 0, a temperatura inicial da placa fria 6 T,= 15°Ce um fluxo térmico uniforme q"=105 W/m2 é aplicado na sua base. Usando o método implícito de diferenças finitas e um incremento de tempo de Aí= 0,1 s, calcule as temperaturas nodais indicadas em função do tempo. A partir das temperaturas calculadas em um tempo específico, calcule a razão entre a taxa de transferência de calor por convecção para a água e a taxa de introdução de calor pela base. Interrompa os seus cálculos quando essa razão atingir o valor de 0,99. Imprima o campo de temperaturas a cada 5 s e no instante no qual os cálculos são interrompidos.
Passo 1
Iai gente! Prontos pra detonar mais uma questão comigo? Bora lá!
O método de balanço de energia deve ser aplicado para cada região nodal. Se a gente agrupar regiões similares, vamos obter os seguintes resultados:
Para os nós 1 e 5:
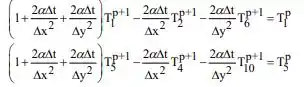
Para os nós 2, 3, 4:
Para os nós 6 e 14:
Para os nós 7 e 15:
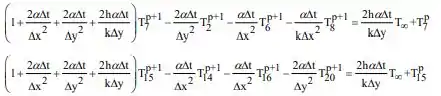
Para os nós 8 e 16:
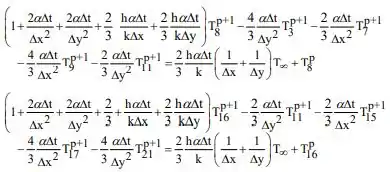
Para o nó 11:
Para os nós 9, 12, 17, 20, 21, 22:
Para os nós 10,13, 18, 23:
Para o nó 19:
Para os nós 24 e 28:
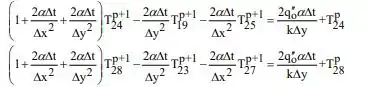
Para os nós 25, 26 e 27:
Passo 2
Portanto, a taxa de convecção de calor é igual a:
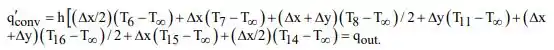
A entrada de calor, por sua vez, é igual a:
E a taxa de introdução de calor pela base será:
Passo 3
Os resultados de cálculos feitos no software foram printados e mostrados a seguir (em °C):
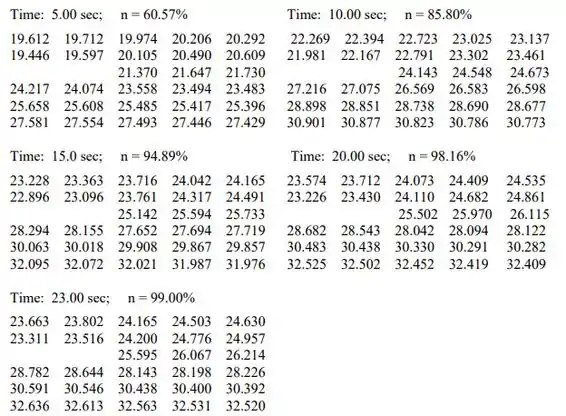
Espero que tenham curtido! Nos vemos na próxima questão, galera!