Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 18

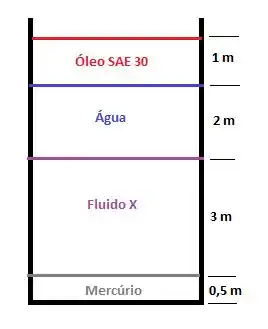
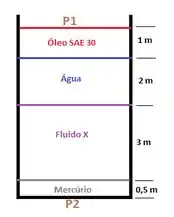
O sistema abaixo está a 20°C. Se a pressão atmosférica é de 101,33 kPa e a pressão no fundo do tanque é de 242 kPa, qual é a densidade do fluido X?

Passo 1

Fala aí, galera!!! Bora pra mais um “lerigou” da mecânica dos fluidos?

Bem, a primeira coisa que a gente tem que saber que isso aí aconteceu por causa do professor das meninas superpoderosas quando “acidentalmente acrescentou o elemento X” (Eu sei que você leu isso com a voz do narrador hehe).

Mas agora falando sério, a primeira coisa que precisamos nessa questão é lembrar do conceito de hidrostática quando nos diz que a pressão em um ponto é igual a soma de todas as pressões estão acima deste mesmo ponto.

P 2 = P 1 + P ó l e o + P á g u a + P f l u i d o   x + P M e r c ú r i o

Passo 2

Nesse momento precisamos então relembrar como que se calcula a pressão de uma coluna de fluido. Se não se lembra, se liga só!

P i = ρ i g h i

Ou seja, para calcular a pressão do fluido i, eu preciso da densidade dele e saber qual é a altura da coluna do fluido i.

Então fechou!!!! Agora é só a gente pegar as densidades dos fluidos (está na tabela ao final do livro) na temperatura dita e voilá!!!

ρ ó l e o = 872   k g / m ³

ρ á g u a = 979   k g / m 3  

ρ f l u i d o   X = ρ x

ρ m e r c ú r i o = 13310   k g / m 3

Passo 3

Agora é mão na massa e usar a nossa velha amiga calculadora!

P 2 = P 1 + P ó l e o + P á g u a + P f l u i d o   x + P M e r c ú r i o

242000 = 101330 + ∑ ρ i g h i

242000 = 101330 + ρ o l e o h o l e o + ρ á g u a h á g u a + ρ x h x + ρ m e r c ú r i o h m e r c ú r i o g

242000 = 101330 + 872 x 1 + 979 x 2 + ρ x   x   3 + 13310   x   0,5 9,81

Resolvendo para ρ x ,   temos ao final ρ x = 1527,3   k g / m ³

Comentário: Perceba que a densidade encontrada faz sentido, uma vez que ela é maior que da água e menor que do mercúrio e o fluido está exatamente entre a coluna de água e de mercúrio.

Resposta

ρ = 1527,3   k g / m ³

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O sistema ar-óleo-água na Figura P2.15 está a 20°C. Sabendo que o manômetro A registra a pressão absoluta de 103,42 kPa e o manômetro B registra 8618 Pa menos do que o manômetro C, calcule (a) o peso
O tubo em U abaixo tem diâmetro interno de 1 cm e contém mercúrio como mostra a figura. Se colocarmos 20 cm³ de água no ramo direito do tubo, qual será a altura da superfície livre em cada ramo após o
O medidor de combustível de um tanque de gasolina de um carro fornece uma indicação proporcional à pressão manométrica do fundo do tanque, como mostra a figura abaixo. Se o tanque tiver 30 cm de profu
Na figura abaixo ambos os fluidos estão a 20°C. Se os efeitos da tensão superficial forem desprezíveis, qual a massa específica do óleo, em kg/m³?
Vênus tem uma massa de 4,90 x 1024 kg e um raio de 6050 km. A atmosfera de Vênus é 96% CO2, mas vamos considerar que seja 100%. A temperatura média na superfície é em torno de 730 K, diminuindo para 2