Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 135

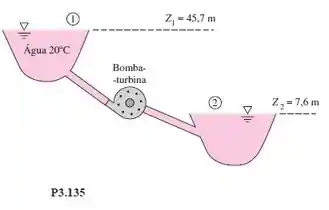
O sistema bomba-turbina da Figura P3.135 retira água do reservatório superior durante o dia para produzir energia elétrica para uma cidade. À noite, o sistema bombeia água do reservatório inferior para o superior para restaurar a situação. Para uma vazão de projeto de 56,8 m³/min em ambas as direções, a perda de carga por atrito é de 5,2 m. Calcule a potência em KW (a) extraída pela turbina e (b) entregue pela bomba.

Passo 1

Bora que essa vai ser moleza!!

Vamos começar fazendo algumas observações. Note que nos pontos 1 e 2, a pressão é exatamente igual, no caso a pressão atmosférica. Por se tratar de dois reservatórios grandes, a velocidade d’gua na superfície destes tende a zero.

  1. – Nesta alternativa a equação de energia tem a forma:

P 1 ρ g + V 1 2 2 g + Z 1 = P 2 ρ g + V 2 2 2 g + Z 2 + h p + h t u r b i n a

Daí, rearranjando a equação obtemos a carga da turbina:

h t u r b i n a = ( P 1 - P 2 ) / ρ g + V 1 2 - V 2 2 2 g + Z 1 - Z 2 - h p

h t u r b i n a = 0 + 0 + 45,7 m - 7,6 m - 5,2 m = 32,9 m

Agora, calcularemos a potência da turbina:

P = ρ g Q h t u r b i n a = 998 k g m 3 * 9,8 m s 2 * 56,8 m 3 m i n * 1 m i n 60 s * 32,9 m = 304613,82 W

≈ 304,614   k W

Passo 2

Agora vamos para o item (b). A única diferença deste para o item (a) é que o sentido da perda de carga por atrito, de modo que a equação de energia fica na forma abaixo:

P 1 ρ g + V 1 2 2 g + Z 1 = P 2 ρ g + V 2 2 2 g + Z 2 - h p + h b o m b a

Daí:

h b o m b a = ( P 1 - P 2 ) / ρ g + V 1 2 - V 2 2 2 g + Z 1 - Z 2 + h p

= 0 + 0 + 45,7 m - 7,6 m + 5,2 m = 43,3 m

Agora, definiremos a potência da bomba:

P = ρ g Q h b o m b a = 998 k g m 3 * 9,8 m s 2 * 56,8 m 3 m i n * 1 m i n 60 s * 43,3 m = 400905,12 W

P ≈ 400,91 k W

Resposta

A potência da turbina solicitada no item (a) é de 304,614   k W e a potência da bomba solicitada no item (b) é de 400,91 k W .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um escoamento incompressível, em regime permanente e sem atrito, da esquerda para a direita sobre um cilindro circular estacionário de raio a , é representado pelo campo de velocidade: V → = U 1 - a r
O campo de velocidade para uma fonte plana a uma distância h acima de uma parede infinita alinhada ao longo do eixo x foi dado no Problema 6.8. Usando os dados desse problema, trace um gráfico da dist
Um bocal de perfil aerodinâmico, com o diâmetro de saída d = 20m m , está acoplado a um tubo reto por meio de flanges. Água escoa no tubo de diâmetro D = 50m m , e o bocal a descarrega para a atmosfer
Água escoa em regime permanente através de um cotovelo redutor, conforme mostrado. O cotovelo é liso e curto e o escoamento acelera, de modo que o efeito do atrito é pequeno. A vazão em volume é Q = 2
Um bocal está acoplado na ponta de uma mangueira de incêndio com diâmetro interno D = 75m m . O bocal é de perfil liso e tem diâmetro de saída d = 25m m . O bocal foi projetado para operar com uma pre