Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 69
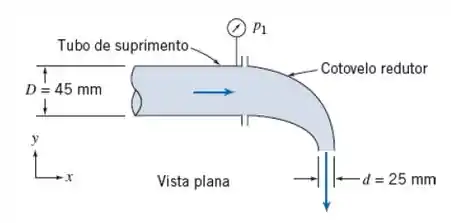
Água escoa em regime permanente através de um cotovelo redutor, conforme mostrado. O cotovelo é liso e curto e o escoamento acelera, de modo que o efeito do atrito é pequeno. A vazão em volume é . O cotovelo está em um plano horizontal. Estime a pressão manométrica na seção 1. Calcule a componente da força exercida pelo cotovelo redutor sobre o tubo de suprimento de água.
Passo 1
Vamos começar esse exercício aplicando o princípio da continuidade, como temos regime permanente e escoamento uniforme, tudo o que entra no cotovelo tem que sair na sua seção de descarga, dessa forma, as vazões são iguais nos pontos de entrada (1) e saída (2), de forma que podemos escrever:
E, podemos calcular a velocidade através da vazão dada, só precisamos convertê-la para m³/s:
Então, a velocidade em 2 será:
E a velocidade 1 será:
Passo 2
Agora vamos aplicar a equação de Bernoulli entre a entrada do cotovelo (1) e sua saída (2), então, temos:
Nesse exercício podemos desprezar a diferença entre as cotas e , e como a seção 2 descarrega para a atmosfera, temos e dessa forma a pressão obtida será a pressão manométrica. Substituindo os valores conhecidos, temos:
Substituindo os valores conhecidos, temos:
Passo 3
Agora vamos aplicar a equação 4.18a de equilíbrio de momento na direção , que é dada por:
No nosso caso, estamos com um regime permanente, então podemos desprezar a primeira integral com a derivada no tempo, vamos desprezar também a ação da força de campo na direção , de modo que , e como estamos trabalhando com pressão manométrica e na seção 2 temos , não teremos força de superfície em 2. Então a equação se torna:
Devido a continuidade, sabemos que:
Então, reescrevendo a equação anterior sabendo também que é a velocidade de entrada e é a velocidade de saída , que não possui componente em , então então:
Substituindo os valores conhecidos, temos:
Essa é a força que o tubo exerce no cotovelo, então a força que o cotovelo exerce no tubo possui mesma intensidade e sentido oposto, dessa forma: