O sistema cilíndrico ilustrado tem variações de temperatura nas direções e desprezíveis. Considere que seja pequena quando comparada a e represente o comprimento na direção , normal à página, por .

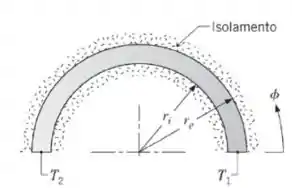
1. Começando pela definição de um volume de controle apropriado e considerando os efeitos de geração e acúmulo de energia, deduza a equação diferencial que descreve a variação da temperatura em função da coordenada angular . Compare seu resultado com a Equação 2.26.
2. Para condições de regime estacionário, sem geração interna de calor e propriedades constantes, determine a distribuição de temperaturas em termos das constantes , , e . Esta distribuição é linear em ?
3. Para as condições do item (b), escreva a expressão para a taxa de transferência de calor, .

A letra a, pede pra gente definir um volume de controle para depois deduzir a equação que descreve a variação da temperatura em função da coordenada angular… Vamos começar então!

Estamos trabalhando com um sistema cilíndrico, então vamos definir o volume de controle como sendo:

Agora vamos usar a conservação de energia:

Opa! Antes de dar continuidade vamos definir com calma quem são esses e … Vamos lá!

e

Agora unindo a equação vamos ficar com o seguinte:

Opa! Olha isso, nossa temperatura é independente de e de , assim como a equação 2.26, show?

Vamos agora para a letra b, que quer saber se a distribuição de temperatura é linear em , assumindo regime estacionário…

Bom, se estamos em regime estacionário, sabemos que:

Mas estamos trabalhando com propriedades constantes, então:

constante

E sendo assim, a distribuição de temperatura é linear com .

Show de bolinhas! Falta só a letra c agora, hein?

Na letra c, precisamos escrever a expressão da taxa de transferência de calor, usando as mesma condições da letra b… Tranquilo?

Vamos usar a lei de Fourier com nosso gradiente de temperatura, ok?

Conseguimos! Arrasamos!