Um cabo elétrico, de raio e condutividade térmica , encontra-se coberto por uma camada isolante cuja superfície externa tem raio e troca calor por convecção e por radiação com o ar circundante e a vizinhança, respectivamente. Quando uma corrente elétrica passa pelo cabo, há geração de energia térmica em seu interior a uma taxa volumétrica .
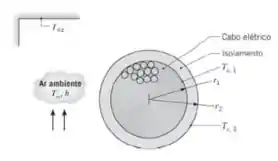
- Escreva as formas da equação da difusão térmica, em regime estacionário, para o isolamento e para o cabo. Verifique se essas equações são satisfeitas pelas seguintes distribuições de temperaturas:
- Utilizando a lei de Fourier, mostre que a taxa de transferência de calor por condução, por unidade de comprimento, através do isolamento pode ser representada por
- Fazendo um balanço de energia em uma superfície de controle colocada ao redor da superfície externa da camada isolante, obtenha uma expressão na qual possa ser determinada em função de , , , , e .
- Considere condições nas quais uma corrente elétrica de atravessa um cabo cuja resistência elétrica por unidade de comprimento é , com um raio e uma condutividade térmica . Para ; ; ; ; e , calcule as temperaturas superficiais, e , bem como a temperatura na linha de centro do cabo.
- Mantendo todas as demais condições, calcule e represente graficamente , e como funções de para .
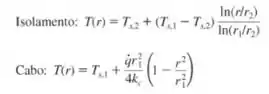
Esboce a distribuição de temperaturas, , no cabo e na camada de isolante, identificando as principais características.
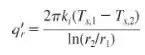
Usando um balanço de energia em uma superfície de controle envolvendo o cabo, obtenha uma expressão alternativa para , escrevendo seu resultado em termos de e .
Passo 1
Fala aí! Partiu fortalecer nossos conhecimentos com essa questão aí!
Só de olhar o tamanho dessa questão dá nem vontade de fazer, né?

Juntos nós damos conta dessa questão gigante! Vamos nessa!
Passo 2
Bom, vamos com pelo começo… Letra a!
Ela ta pedindo pra gente escrever a equação da difusão térmica para o isolamento e para o cabo… Vamos começar pelo isolamento, assumindo estado estacionário… E ver se a distribuição de temperaturas dada satisfaz ela:
Como nossa expressão dentro do colchete não depende de , então sim! satisfaz a equação!
Agora vamos fazer o mesmo para o cabo!
Nossa expressão dentro do parêntese não depende de , então sim! satisfaz a equação!
Passo 3
Além disso a letra a pediu pra gente identificar as características da temperatura …
Bom, temos quatro pontos diferentes durante a curva para avaliar…
O primeiro é quando o gradiente é zero, pois ainda não sofreu alteração de temperatura, depois temos que quanto maior a temperatura também maior será o raio, na terceira parte temos uma descontinuidade e imediatamente depois temos uma queda de temperatura com aumento do raio… Show?
Agora vamos seguir para a letra b!
Passo 4
No caso da letra b, o enunciado pede pra gente mostrar que, partindo da lei de Fourier, a taxa de transferência de calor por condução é dada pela equação que ele nos apresentou… Bom, vamos testar!
A lei de Fourier diz o seguinte:
Substituindo nossa distribuição de temperatura:
Opa! Conseguimos mostrar o que a questão queria… Mas ainda não acabou por aí… A letra b, ainda pede para fazer um balanço de energia, pra gente conseguir uma expressão alternativa para …
Bom, o nosso balanço de energia ficaria assim:
Conseguimos! Acabamos com a letra b!
Passo 5
Na letra c, precisamos fazer um balanço de energia em uma superfície de controle coincidente com a superfície externa da camada de isolamento… Vamos lá!
E para deixar em função das variáveis que o enunciado pediu, precisamos substituir a área e o que achamos no passo anterior!
Prontinho! A letra c já foi!
Passo 6
Agora vamos de letra d…
Ela nos dá vários dados e pede pra gente calcular as temperaturas no reator e na superfície externa do isolamento, ou seja, ela quer o e o !
Pra fazer isso precisaremos usar as equações que desenvolvemos até agora, beleza?
Vamos começar usando a equação do passo 4 para encontrar o nosso :
ou
Show! Agora podemos substituir o valor de na equação da primeira parte do passo 4:
ou
Agora só falta o … Vamos nessa!
Uhul! Só a letra e agora!
Passo 7
A letra e, quer que a gente faça um gráfico de ou em função de , com a seguinte condição:
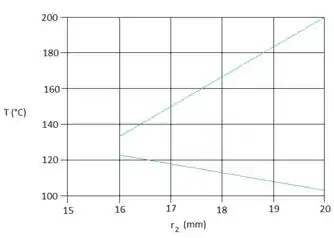
Sendo a curva azul correspondente a parte interna e a curva verde a parte externa.
Show!! Arrasamos!!
Resposta
Ei, a resposta está no passo a passo :)