Uma mistura quimicamente reativa é armazenada em um recipiente esférico com paredes finas, de raio . A reação exotérmica gera calor a uma taxa volumétrica uniforme, porém dependente da temperatura na forma , sendo , e a temperatura da mistura em kelvins. O recipiente é envolto por uma camada de material isolante que tem raio externo , condutividade térmica e emissividade . A superfície externa do isolamento troca calor por convecção e radiação com o ar adjacente e uma grande vizinhança, respectivamente.
- Escreva a forma no estado estacionário da equação da difusão térmica para o isolante. Verifique se essa equação é satisfeita pela seguinte distribuição de temperaturas
- Utilizando a lei de Fourier, mostre que a taxa de transferência de calor por condução através do isolamento pode ser representada por
- Fazendo um balanço de energia em uma superfície de controle coincidente com a superfície externa da camada de isolamento, obtenha uma expressão na qual possa ser determinada em função de , , , , e .
- O engenheiro de processos deseja manter a temperatura no reator em em condições nas quais ; ; ; ; e . Quais são as temperaturas reais no reator e na superfície externa do isolamento térmico, ?
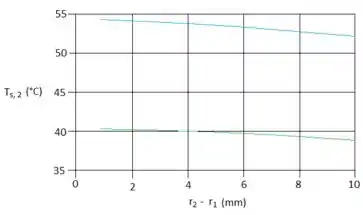
- Calcule e represente graficamente a variação de em função de para . O engenheiro está preocupado com eventuais acidentes por queimadura que possam ocorrer com o pessoal que entrar em contato com a superfície exposta do isolante térmico. O aumento da espessura da camada de isolamento térmico é uma solução prática para manter ? Que outro parâmetro poderia ser alterado para reduzir o valor de ?
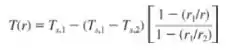
Esboce a distribuição de temperaturas, , identificando as suas principais características.
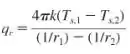
Fazendo um balanço de energia em uma superfície de controle envolvendo o recipiente, obtenha uma expressão alternativa para , apresentando seu resultado em termos de e .
Passo 1
Fala aí! Partiu fortalecer nossos conhecimentos com essa questão aí!
Só de olhar o tamanho dessa questão dá nem vontade de fazer, né?

Brincadeiras a parte, relaxa que juntos nós damos conta dessa questão gigante! Vamos nessa!
Passo 2
Bom, vamos com pelo começo… Letra a!
Ela ta pedindo pra gente escrever a equação da difusão térmica para o isolante, assumindo estado estacionário… E ver se a distribuição de temperaturas dada satisfaz ela, vamos ver então!
Como nossa expressão dentro do colchete não depende de , então sim! satisfaz a equação!
Além disso a letra pediu pra gente identificar as características da temperatura …
Bom, a primeira coisa que podemos notar é que , beleza? E além disso quanto maior o raio menor será nossa temperatura, show?
Agora vamos seguir para a letra b!
Passo 3
No caso da letra b, o enunciado pede pra gente mostrar que, partindo da lei de Fourier, a taxa de transferência de calor por condução é dada pela equação que ele nos apresentou… Bom, vamos testar!
A lei de Fourier diz o seguinte:
Substituindo nossa distribuição de temperatura:
Opa! Conseguimos mostrar o que ele queria… Mas ainda não acabou por aí… A letra b, ainda pede para fazer um balanço de energia, pra gente conseguir uma expressão alternativa para …
Bom, o nosso balanço de energia ficaria assim:
Conseguimos! Acabamos com a letra b!
Passo 4
Na letra c, precisamos fazer um balanço de energia em uma superfície de controle coincidente com a superfície externa da camada de isolamento… Vamos lá!
E para deixar em função das variáveis que o enunciado pediu, precisamos substituir a área …
Prontinho! A letra c já foi!
Passo 5
Agora vamos de letra d…
Ela nos dá vários dados e pede pra gente calcular as temperaturas no reator e na superfície externa do isolamento, ou seja, ela quer o e o !
Pra fazer isso precisaremos juntar as equações que desenvolvemos até agora e montar um sistema, beleza?
Vamos começar com a equação da taxa de condução do isolamento, que encontramos lá na primeira parte do passo 3:
Agora a equação da segunda parte do passo 3:
E por último a equação final do nosso passo 4:
Agora podemos substituir nossa segunda equação na terceira e ficar com:
E montar um sistema com a primeira equação, onde vamos ter duas equações e duas incógnitas… Dessa forma a gente acha que:
e
Agora só falta a última letrinhas… Vamos nessa!
Passo 6
A letra e, quer que a gente faça um gráfico de em função de , com a seguinte condição:
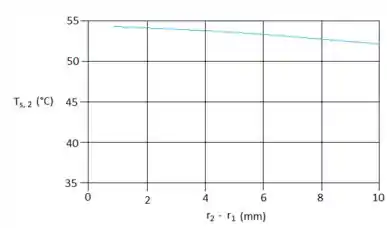
Além disso, a questão pergunta também qual parâmetro poderia ser alterado para diminuir nosso … Bom, se a gente aumenta nosso conseguiremos fazer isso, podemos comprovar observando a curva verde no nosso gráfico!
Resposta
Ei, a resposta está no passo a passo :)