Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 4.Exercício - Ex. 29

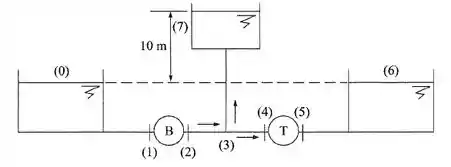
No sistema da figura, a bomba deve fornecer 10 L/s ao reservatório superior e a turbina deve ter uma potência no eixo de 3 kW com um rendimento de 80%. Qual é a carga manométrica da bomba e a da turbina? Dados: H p 0,1 = 2   m ; H p 2,3 = 4   m ; H p 3,4 = 4   m ; H p 5,6 = 4   m ; H p 3,7 = 2 m ;   H p 3 = 0 ; N B = 7,5   k W ; γ = 10 4   N / m 3 ; η B = 0,8 .

Passo 1

Vamos começar o exercício calculando a potência no ponto 1 e no ponto 2, que são dadas por (lembrando que a potência no ponto 1 é a líquida da bomba e no ponto 2 temos a potência bruta fornecida a turbina):

N 1 = N B η B = 7,5 0,8 → N 1 = 6   k W

N 2 = N T η T = 3 0,8 → N 2 = 3,75   k W

Passo 2

Agora vamos usar o princípio da conservação da energia para o sistema, assim, temos:

γ Q 0 H 0 + N 1 - N 2 = γ Q 6 H 6 + γ Q 7 H 7 + γ Q 0 H p 0,1 + γ Q 0 H p 2,3 + γ Q 6 H p 3,4 + γ Q 6 H p 5,6 + γ Q 7 H p 3,7

Agora vamos substituir os valores conhecidos na equação:

10 4 Q 0 0 + 6000 - 3750 = 10 4 Q 6 0 + 10 4 10.10 - 3 10 + 10 4 Q 0 2 + 10 4 Q 0 4 + 10 4 Q 6 4 + 10 4 Q 6 4 + 10 4 10.10 - 3 2

Simplificando a expressão, temos:

2250 = 1000 + 6 . 10 4 Q 0 + 8 . 10 4 Q 6 + 200 → 6.10 4 Q 0 + 8.10 4 Q 6 = 1050

Essa será nossa equação 1. Agora, olhando para o sistema, sabemos que a vazão em 0 é a soma da vazão em 6 mais a vazão fornecida pela bomba em 7, dessa forma, temos:

Q 0 = Q 6 + Q 7 → Q 0 = Q 6 + 0,01

Passo 3

Agora substituindo o valor de Q 0 encontrado na equação 1, temos:

6.10 4 Q 0 + 8.10 4 Q 6 = 1050 → 6.10 4 Q 6 + 0,01 + 8.10 4 Q 6 = 1050

Q 6 = 3,2.10 - 3   m 3 / s

E, substituindo esse valor na expressão para Q 0 :

Q 0 = Q 6 + 0,01 = 3,2.10 - 3 + 0,01 → Q 0 = 13,2.10 - 3   m 3 / s

Agora, podemos reescrever a equação para a potência da bomba em função de sua carga como:

N B = γ Q 0 H B η B → H B = N B η B γ Q 0 = 7500 0,8 10 4 13,2.10 - 3 → H B = 45,4   m

E, da mesma forma, para a turbina:

N T = γ Q 6 H T η T → H T = N T γ Q 6 η T = 3000 10 4 3,2.10 - 3 0,8 → H T = 117,2   m

Resposta

H B = 45,4   m

H T = 117,2   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a água no tubo do Problema 6.89 está inicialmente em repouso e a pressão é mantida em 10,3 kPa (manométrica), deduza uma equação diferencil para a velocidade V no tubo como uma função do tempo, int
Considere o tanque do Problema 4.46. Usando a equação de Bernoulli para escoamente não permanente ao longo de uma linha de corrente, avalie a mínima razão entre diâmetros, D / d , necessária para just
Esboce cuidadosamente as linhas de energia (LE) e as linhas piezométricas (LP) para o sistema mostrado na Fig. 6.6, se uma bomba (adicionando energia ao fluido) estiver localizada no ponto 2, ou no po
Esboce cuidadosamente as linhas de energia (LE) e as linhas piezométricas (LP) para o sistema mostrado na Fig. 6.6, se o tubo for horizontal (isto é, a saída está na base do reservatório) e uma turbin
Dois discos circulares, de raio R, estão separados pela distância b . O disco superior se move em direção ao inferior com uma velocidade constante V . O espaço entre eles está cheio de um líquido sem