Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 70
A água a 20 °C escoa através de um tubo longo e reto. A queda de pressão é medida ao longo de uma seção do tubo de comprimento = 1,3 m como uma função da velocidade média no tubo (Tabela P7-70). O diâmetro interno do tubo é = 10,4 cm. (a) Adimensionalize os dados e trace o número de Euler como uma função do número de Reynolds. A experiência foi executada a velocidades suficientemente altas para atingir a independência do número de Reynolds? (b) Extrapole os dados experimentais para prever a queda de pressão a uma velocidade média de 80 m/s.
Passo 1
Vamos começar definindo as hipóteses para o nosso problema:
- O escoamento é completamente desenvolvido
- O escoamento é permanente e incompressível
Para a água a uma temperatura de 20 °C e na pressão atmosférica, temos que kg/m³ e kg/ms.
Vamos analisar os dados através da adimensionalização dos mesmos através dos números de Reynolds e Euler.
Passo 2
O número de Euler e o número de Reynolds são dados por:
A tabela abaixo mostra os valores para os dois números adimensionais
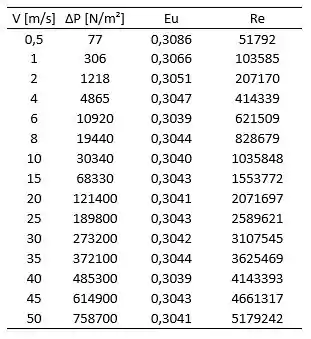
Assim, podemos traçar o gráfico de Euler em função de Reynolds, como pode ser observado logo abaixo:
Analisando o gráfico podemos concluir que o experimento atingiu a independência do número de Reynolds em altas velocidades, visto que o número de Euler não sofre variações significativas a partir de . Além disso, podemos obter um número de Euler médio para altas velocidades:
Passo 3
Vamos extrapolar a pressão para altas velocidades. Vamos assumir que em velocidades mais altas, o número de Euler mantém-se constante e igual ao valor médio de 0,3042. Com isso temos que a pressão para uma velocidade de 80 m/s é:
Resposta
(b)