Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 6.Problemas - Ex. 34
Usando as análises do Exemplo 6.1 e do Problema 6.32, trace um gráfico da discrepância (percentual) entre as vazões obtidas a partir da consideração de escoamento uniforme e perfil de vórtice (irrotacional) livre em função do raio interno r1.
Passo 1
Pessoal, a equação de vazão é dada por:
Pelo exemplo 6.1, tiramos que:
A vazão uniforme é dada então por:
Isolando os raios, temos:
Já no Problema 6.32, considerando o perfil em vórtice irrotacional, temos:
Isolando os raios, temos:
Passo 2
Vamos agora comparar a discrepância através de alguns valores para , via excel:
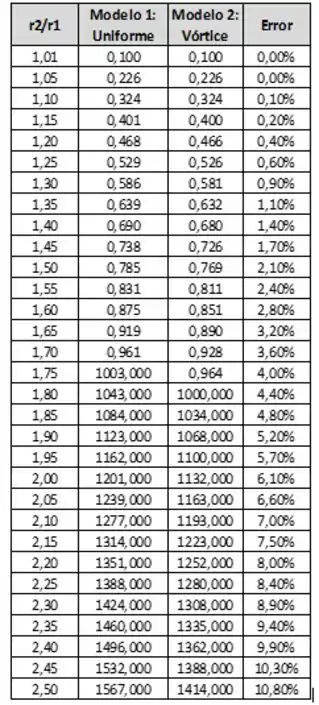
Traçando um gráfico dos erros, temos:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
6.4 Um campo de velocidade em um fluido com massa específica de 1000 kg/m³ é dado por V → = - A x + B y t i ^ + A y + B x t j ^ , em que A = 2s - 1 , B = 1m / s 2 , x e y são em metros e t é em segund
6.3 Um escoamento horizontal de água é descrito pelo campo de velocidade V → = - A x + B t i ^ + A y + B t j ^ , em que A = 1s - 1 , B = 2m / s 2 , x e y são em metros e t é em segundos. Encontre expr
6.1 Considere o campo de escoamento com velocidade dada por V → = A y 2 - x 2 - B x i ^ + 2 A x y + B y j ^ em que A = 3,28m - 1 s - 1 , B = 3,28m - 1 s - 1 e as oordenadas são medidas em metros. A ma
6.5 Considere o campo de escoamento com velocidade dada por V → = A x 2 - y 2 - 3 B x i ^ + 2 A x y - 3 B y j ^ , em que A = 3,28s - 1 , B = 1m / s 2 e as coordenadas são medidas em metros. A massa es
6.6 A componente em x da velocidade em um campo de escoamento incompressível é dada poru = A x , em que A = 2s - 1 e as coordenadas são medidas em metros. A pressão no ponto (x,y)=(0,0) é p 0 = 190k P