Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 93
Uma sonda de filme quente é montada sobre um sistema cone-barra em um fluxo de ar de 45 m/s, ao nível do mar, como na Figura P7.93. Calcule o ângulo máximo admissível do vértice do cone, sabendo que o momento fletor induzido pelo escoamento na base da barra não
deve exceder 30 N cm.
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Nessa questão, temos um sistema-cone barra em um fluxo de ar de velocidade , como demonstra a imagem que ilustra o problema.
Como podemos ver, a barra tem comprimento e diâmetro . Já o cone tem diâmetro .
O enunciado nos pede pra calcular o ângulo máximo admissível do vértice do cone pra o qual o momento fletor não exceda .
Pra isso, vamos ter que fazer um balanço de momento entre as forças de arrasto agindo tanto no cone quanto na barra.
Nos próximos passos vou te mostrar como calcular esses momentos e como achar o ângulo máximo para o vértice do cone.
Mas antes da gente ir pro Passo 2, vamos lembrar que para o ar à temperatura ambiente, a massa específica será e a viscosidade será .
Agora sim, vem comigo pra gente matar esse problema juntos!
Passo 2
Em primeiro lugar, vamos calcular o momento devido à força de arrasto da barra
Pra isso, vamos lembrar que a força de arrasto é dada por:
Sendo a área frontal da barra.
Para calcular o coeficiente de arrasto , devemos antes calcular o número de Reynolds para o escoamento:
Considerando a barra como um cilindro circular liso, podemos ir no gráfico da figura 7.16(a) na página 492, onde entramos com o número de Reynolds encontrado e achamos:
Sendo assim, o coeficiente de arrasto para este problema é .
Agora podemos calcular a força de arrasto da barra:
Pra calcular o momento dessa força com relação à base da barra, vamos considerar a barra uniforme e, portanto, considerar que toda a força de arrasto nessa barra está aplicada em seu centro.
Logo, a distância da aplicação da força de arrasto até a base da barra é . Sendo assim, o mento na barra se torna:
Passo 3
Para encontrar a força de arrasto no cone, precisaríamos do seu coeficiente de arrasto , mas, de acordo com a Tabela 7.3 na página 495, nos precisamos saber o ângulo do vértice do cone, que é justamente o que queremos descobrir.
Ou seja, teremos que deixar a força de arrasto em função de da seguinte maneira:
Pra calcular o momento dessa força com relação à base da barra, vamos considerar o cone uniforme e, portanto, considerar que toda a força de arrasto no cone está aplicada em seu centro.
Sendo assim, a distância de aplicação da força de arrasto no cone até a base da barra é . Sendo assim, o mento no cone se torna:
Passo 4
Pra finalizar a questão, vamos fazer o balanço de momento de todo o sistema em relação à base da barra.
Devemos lembrar que o somatório do momento deve ser igual a , segundo o enunciado:
Sendo assim, resolvendo pra encontramos:
Sendo assim, vamos dar uma olhada na Tabela 7.3 na página 495:
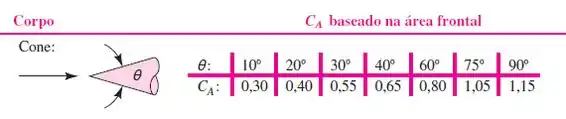
Logo, para esse valor de o ângulo do vértice do cone é
Pronto, matamos a questão juntos!
Resposta
O ângulo do vértice do cone é