Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 108
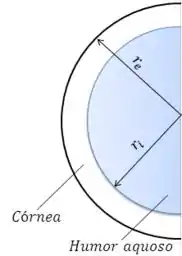
O olho humano contém humor aquoso, que separa a córnea externa da estrutura interna íris-cristalino. Supõe-se que em alguns indivíduos pequenas lascas de pigmento sejam liberadas intermitentemente da íris e migram para a córnea e, em sequência, a danificam. Aproximando a geometria da cavidade formada pela córnea e a estrutura íris-cristalino como um par de hemisférios concêntricos de raio externo e raio interno , respectivamente, investigue se pode ocorrer convecção natural no humor aquoso, estimando a razão efetiva de condutividades térmicas, . Se a convecção natural puder ocorrer, é possível que as partículas danosas sejam arrastadas da íris para a córnea. A estrutura íris-cristalino encontra-se na temperatura corporal, , enquanto a temperatura da córnea foi medida, sendo igual a . As propriedades do humor aquoso são , , , e .
Passo 1
Nossa situação é a seguinte: temos que o olho humano possui duas estruturas, a córnea e o humor aquoso. Aproximando o olho para a geometria de metade de uma esfera, temos que as dimensões dessas duas estruturas são e .
Em algumas pessoas os pigmentos da íris podem migrar para a córnea, causando complicações na visão. Para as condições do problema devemos verificar se seria possível ocorrer a movimentação destes pigmentos, como resultado do processo de convecção natural.
Para fazer isso, precisamos obter a razão , sendo que para a convecção natural não é relevante para o processo. Vamos lá?
Passo 2
A primeira coisa a se fazer será calcular o comprimento característico para o espaço entre humor aquoso e córnea. Para uma região confinada esférica ele é dado por:
Já recebemos as propriedades do humor aquoso no enunciado. Então, temos condições de calcular o número de Rayleigh:
Passo 3
A partir do número de Rayleigh podemos aplicar a seguinte correlação válida para espaços esféricos confinados:
Então, como encontramos que , significa que a convecção natural ocorre nestas condições, podendo arrastar as partículas de pigmento para a córnea.
Resposta
; desta forma, existe o movimento de convecção natural no interior do espaço entre córnea e humor aquoso, o que pode levar ao arraste de partículas danosas para a córnea.