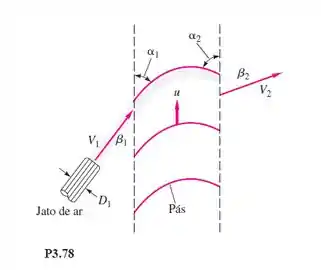
Um jato de fluido de diâmetro D 1 entra em uma grade de pás móveis à velocidade absoluta V 1 e ângulo β 1 , e sai à velocidade absoluta V 2 e ângulo β 2 , como na Figura P3.78. As pás movem-se à velocidade u. Deduza uma fórmula para a potência P entregue às pás em função desses parâmetros.

P = 1 2 m ˙ j a t o ( V 1 2 - V 2 2 )

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 78

Um jato de fluido de diâmetro entra em uma grade de pás móveis à velocidade absoluta e ângulo , e sai à velocidade absoluta e ângulo , como na Figura P3.78. As pás movem-se à velocidade u. Deduza uma fórmula para a potência P entregue às pás em função desses parâmetros.

Passo 1

Bora lá pra mais uma!

Queremos uma expressão para potência, vamos partir da seguinte fórmula para calcular potência:

em que, é a velocidade das pás, no caso, u! Assim,

Passo 2

Vamos tentar achar , para isso, vamos olhar o seguinte esqueminha.

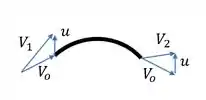
Cara, note que nossa não pega direitinho nas pás, assim, vamos colocar uma certa velocidade relativa , encontraremos ela a partir da lei dos cossenos, assim:

Isolando :

Passo 3

Agora, vamos fazer o balanço do momento do fluido pela direção do movimento das lâminas, ou seja, no sentido de y. Assim,

Daí, substituindo na expressão de potência:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tubo (2)-(3) da figura está ligado ao tanque por meio de uma junta elástica de borracha que impede a transferência de esforços entre o tanque e o tubo. Calcular a altura h do nível de água do tanque

Calcular o esforço horizontal sobre a estrutura do ventilador da figura e a potência transmitida ao fluido pelo ventilador. Desprezar a perda de carga entre as seções (1) e (2). Dados: D 2 = 0,38m ; v

Calcular a força horizontal aplicada sobre o suporte do bocal da figura. Sabendo que a água incide na placa, plana e vertical, e se distribui igualmente em todas as direções, calcular a força que deve

No trecho (1)-(2) da tubulação, que está num plano horizontal, escoa água em regime permanente. A perda de carga de (1) a (2) é 10 m e a vazão, 10 L/s. Qual é a força resultante aplicada pelo fluido n

An observer at sea level does not hear an aircraft flying at12,000-ft standard altitude until it is 5 (statute) mi past her.Estimate the aircraft speed in ft/s.