Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 14
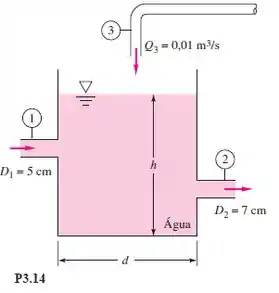
O tanque aberto da Figura contém água a e está sendo enchido através da seção . Considere o escoamento incompressível. Primeiro, deduza uma expressão analítica para a taxa de variação do nível d’água, , em termos das vazões e do diâmetro do tanque, arbitrários. Em seguida, se o nível d’água for constante, determine a velocidade na saída, , para os dados e .
Passo 1
E aí, tudo bem? Bora resolver mais essa comigo!
a)
Vamos matar essa questão tipo o flash, que tal fecharmos o tanque como um volume de controle, assim:
Isolando temos:
Passo 2
b)
Se é constante, temos:
Substituindo pelos valores dados:
Resolvendo encontramos que:
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
a)
b)
Exercícios de Livros Relacionados
Um agricultor está pulverizando um líquido através de 10 bocais com diâmetro interno de 3 mm, a uma velocidade média na saída de 3 m/s. Qual é a velocidade média na entrada do alimentador que possui d
Obtenha expressões para a vazão volumétrica e para o fluxo de quantidade de movimento através da seção transversal do volume de controle mostrado no diagrama.
A distribuição de velocidades para escoamento laminar em um longo tubo circular de raio R é dada pela expressão unidimensional, V → = u i ^ = u m a x 1 - r R 2 i ^ Para este perfil, obtenha expressões
Um laboratório universitário deseja construir um túnel de vento de vazão 15 m 3 s com velocidades variáveis do ar. Para isso, propõe-se construir o túnel com uma sequência de três seções de teste circ
A área sombreada mostrada está em um escoamento onde o campo de velocidade é dado por V =a x î=b y ĵ î ĵ; a=b=1s - 1 e as coordenadas são medidas em metros. Avalie a vazão volumétrica e o fluxo de qua