Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 13
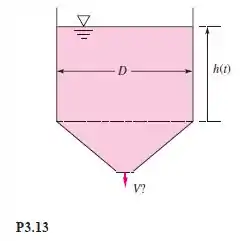
O recipiente cilíndrico da Figura tem de diâmetro e uma contração cônica no fundo com um furo de saída dede diâmetro. O tanque contém água limpa nas condições padrão ao nível do mar. Se a superfície da água estiver descendo a uma taxa aproximadamente constante de , calcule a velocidade média para fora na saída inferior.
Passo 1
E aí, tudo bem? Bora resolver mais essa comigo!
Vamos matar essa questão tipo o flash, podemos considerar que aproximando nosso sistema a um volume de controle, assim:
Isolando e removendo , temos:
Isso é tudo pessoal, conseguimos mais uma! \o/
Resposta
Exercícios de Livros Relacionados
O campo de velocidades de um escoamento bidimensional é dado por v x = 3 + 2 x y + 4 t 2 , v y = x y 2 + 3 t . Determinar os módulos da velocidade e aceleração no ponto 2 ; 1 no instante t = 5s .
UM escoamento é definido pelo campo de velocidades v x = 2 ( 1 + t ) , v y = 3 1 + t , v z = 4 1 + t . Qual é o módulo da velocidade no ponto 3 ; 1 ; 4 no instante t = 2s ? Qual é o módulo da aceleraç
Exercício anterior com v x = 0 , v y = 3 x y e ponto de coordenadas ( 2 ; 2 ) .
Exercício anterior com v x = - 2 y , v y = 3 x e ponto de coordenadas ( 2 ; 3 ) .
Para o escoamento do Problema 4.15, obtenha uma expressão para o fluxo de energia cinética, ∫ ( V 2 2 )ρ V → d A → através da seção 1 transversal do volume de controle mostrado.