Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 15

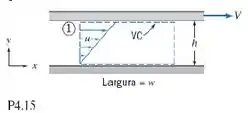
Obtenha expressões para a vazão volumétrica e para o fluxo de quantidade de movimento através da seção transversal do volume de controle mostrado no diagrama.

Passo 1

Essa questão é uma dedução através da figura. Tudo o que temos é um volume de controle com distribuição linear de velocidade em um tubo. Então é necessário determinar a taxa de fluxo de volume e fluxo de momento, aplicando as expressões para fluxo de volume e momento.

A vazão volumétrica através de uma seção de uma superfície de controle A é dada por

Q = ∫ V → d A →

Enquanto o fluxo de momento é:

m f = ρ ∫ V → ( V → d A → )

Passo 2

Considerando um fluxo incompressível, o perfil de velocidade linear se da na direção y de acordo com a altura, logo

V → = V h y i ^

Como aréa tende a diminuir quando y aumenta, o diferencial de área é

d A = - w d y i ^

Assim, para a vazão do volume, temos

Q = ∫ y = 0 y = h V h y 2 i ^   ( - w d i ^ )

Q = - V w h y 3 3 0 h

Q = - V w h h 3 3 - 0             ∴           Q = - 1 3 V w h 2

Prontinho!!

Passo 3

Vamos agora calcular o fluxo da quantidade de movimento. A fórmula para isso, como já vimos ali em cima é:

m f = ρ ∫ V → ( V → d A → )

Vamos fazer as mesmas substituições que fizemos no paço anterior:

V → = V h y i ^

d A = - w d y î

Logo:

m f = ρ ∫ y = 0 h V h y î - V w h y d y

Vamos colocar tudo que é constante para fora da integral:

m f = - ρ V 2 w h 2 î ∫ y = 0 h y d y = - ρ V 2 w h 2 î y 2 2 0 h = - ρ V 2 w 2 î

Resposta

  Q = - 1 3 V w h 2

m f = - ρ V 2 w 2 î

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fluido incompressível escoa em regime permanente pelo duto retangular da figura a seguir. O perfil de velocidades na saída é dado aproximadamente por u = u m á x 1 - y 2 b 2 1 - z 2 h 2 á (a) Esse
O escoamento permanente incompressível entre placas paralelas tem velocidade uniforme na entrada u = U o = 8c m / s , desenvolvendo-se a jusante num perfil laminar parabólico, u = a z z o - z , em que
Modifique o problema P3.16 da seguinte maneira: Considere que a placa tenha comprimento L = 125 δ da entrada até a saída. A placa é porosa e está retirando fluido da camada-limite a uma velocidade de
Água de uma drenagem pluvial escoa para uma saída sobre um leito poroso que absorve a água a uma velocidade vertical uniforme de 8 mm/s, como mostra abaixo. O sistema tem 5 m de largura normal ao pape
Água, admitida incompressível, escoa em regime permanente pelo tubo como mostra abaixo. A velocidade na entrada é constante, u = U o , e a velocidade na saída se aproxima do perfil para escoamento tur