Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 3.Exercício - Ex. 7
Um tubo admite água num reservatório com uma vazão de . No mesmo reservatório é trazido óleo por outro tubo com uma vazão de . A mistura homogênea formada é descarregada por um tubo cuja seção tem uma área de . Determinar a massa específica da mistura no tubo de descarga e sua velocidade.
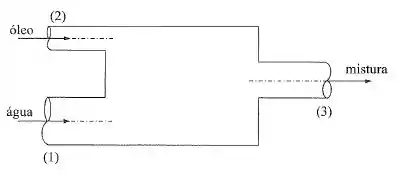
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Pela equação da continuidade, sabemos que a vazão mássica que entra no tubo é igual a vazão que sai, logo:
Como:
Temos que:
Passo 2
Para descobrir a densidade da mistura, temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
Uma mangueira de incêndio tem um diâmetro interno de 125 m m e água está escoando a 2,271 m 3 / m i n . O escoamento sai através de um bocal com um diâmetro D n . Para escoamento permanente, qual deve
Três tubos forncecem água em regime permanente a 20 ° C para um tubo maior de saída mostrado na figura P3.8. A velocidade V 2 = 5 m / s e a vazão de saída Q 4 = 120 m 3 / h . Encontre: V 1 ; V 3 ; V 4
Um tanque esférico, com diâmetro de 35c m , está perdendo ar através de um furo de 5m m de diâmetro na sua lateral. O ar sai pelo furo a 360m / s com massa específica de 2,5k g / m 3 . Supondo uma mis
Quando um jato líquido, regido pela gravidade, sai de uma fenda em um tanque, como na Figura P 3.6 , uma aproximação para a distribuição de velocidade na saída é u ≈ 2 g h - z 1 2 , onde h é a profund
Estenda o Problema P3.92 para incluir o atrito na parede devido a uma tensão de cisalhamento média linear (laminar) na forma τ ≈ c V , em que c é uma constante. Encontre a equação diferencial para dV/