Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 4.Problemas - Ex. 85

Uma placa plana de largura e extensão infinitas oscila senoidalmente sobre seu próprio plano embaixo de um fluido viscoso, como mostrado abaixo. O fluido está em repouso bem acima da placa. Adotando o máximo possível de hipóteses simplificadoras, escreva a equação diferencial governamental e as condições de contorno para determinar o campo de velocidade u no fluido. Não resolva!!!

Passo 1

Tudo bem, genteee?!! Então, vamos começar nossas aventuras com a mecânica dos fluidos?

Vamos assumir que u = u ( y , t ) e que d p d x = 0 , uma vez que temos que nosso escoamento está na direção x.

A relação de momento na direção x se torna então:

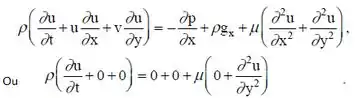
Ou finalmente, temos que:

∂ u ∂ t = μ ρ ∂ 2 u ∂ y 2

Passo 2

Bem, as nossas condições de contorno nesse problema são de boa de visualizar, porque em cima da placa, ou seja, em y = 0, temos a velocidade igual a velocidade do prato.

u 0 , t = U 0 s e n ω t

E quando estivermos muiiiiitooo longe do prato, você concorda comigo que o fluido nem vai sentir ou perceber que tem um prato se movendo ali, ou seja, o fluido vai ficar paradinho!!!

u ∞ , t = 0

Resposta

∂ u ∂ t = μ ρ ∂ 2 u ∂ y 2

u 0 , t = U 0 s e n ω t

u ∞ , t = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere o escoamento estacionário da água através do bocal de uma mangueira de jardim assimétrico . Ao longo do eixo central do bocal, a velocidade da água aumenta de u e n t r a d a para u s a í d
Cite e descreva brevemente os quatro tipos fundamentais de movimento ou deformação das partículas de fluido.
O escoamento de duto convergente (Figura P4-15) é modelado pelo campo de velocidade em regime permanente e bidimensional do Problema 4-15. Esse campo de escoamento é rotacional ou irrotacional? Mostre
Usando os resultados do Problema 4-43 e a definição fundamental da taxa de deformação linear (a taxa de aumento do comprimento por unidade de comprimento), deduza uma expressão para a taxa de deformaç
O escoamento de duto convergente é modelado pelo campo de velocidade em regime permanente e bidimensional do Problema 4-15. Como o escoamento é simétrico com relação ao eixo x , o segmento de reta A B