A água entra em uma bomba centrífuga de forma axialmente à pressão atmosférica, a uma taxa de e a uma velocidade de , e sai na direção normal ao longo da carcaça da bomba, como mostra a Figura P6-37. Determine a força que age sobre o eixo (que também é a força que age sobre o rolamento do eixo) na direção axial.

Passo 1
O problema quer saber o valor da força resultante que age sobre o eixo da bomba. Para descobrir isso, precisamos primeiro determinar o volume de controle que estudaremos. Como queremos informações sobre o eixo da bomba, vamos considerar que o volume de controle é a reião do espaço que engloba a bomba. A figura abaixo mostra isso.
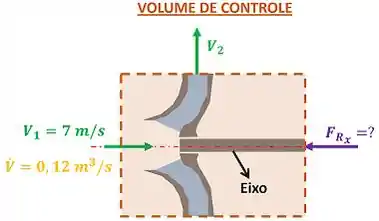
é a vazão volumétrica de água através da bomba, é a velocidade da água que entra no volume de controle e é a velocidade da água que sai do volume de controle.
No próximo passo, aprenderemos a calcular .
Passo 2
Para encontrar uma expressão para a força , temos que usar a segunda lei de Newton (equação da quantidade de movimento) para escoamentos em regime permanente. Segue abaixo a equação da segunda lei para o volume de controle.
onde é o somatório de todas as forças que atuam no eixo , é a vazão mássica do líquido que passa pelo volume de controle e é o fator de correção do escoamento. O fator de correção para escoamentos turbulentos é próximo de . Como o escoamento através de bombas é geralmente turbulento, podemos admitir que vale .
é a componente horizontal da velocidade da água entrando no volume de controle. Como a água entrando no volume de controle só possui uma velocidade horizontal , vale:
é a componente horizontal da velocidade da água saindo do volume de controle. Como a água saindo do volume de controle só possui velocidade vertical, sua componente horizontal, vale:
Passo 3
Neste momento, precisamos lembrar que é a força resultante que age sobre o eixo . Logo:
O sinal de menos é porque o sentido da força é da direita pra esquerda.
Para fechar, a vazão mássica de um escoamento incompressível é a multiplicação entre a vazão volumétrica e a densidade . Como o escoamento através da bomba é de líquido e o líquido é aproximadamente incompressível, podemos considerar esse escoamento incompressível. Por isso:
A densidade da água líquida a pressão atmosférica vale aproximadamente .
Substituindo tudo isso na segunda lei:
Passo 4
Substituindo todos os dados na fórmula de , encontramos: