Reconsidere o Problema 6-32. Usando o EES (ou outro software) investigue o efeito da velocidade da placa sobre a força exercida na placa. Faça a velocidade da placa variar de a em incrementos de . Tabule e represente graficamente os resultados.
Passo 1
A questão pede que a gente avalie a influência da velocidade da placa sobre a força que o jato exerce sobre a placa. Para isso, o primeiro passo será lembrar do Problema 6-32 através da figura abaixo.

é a velocidade do jato de água que atravessa o volume de controle em relação ao chão e é a velocidade da placa.
é a força que a placa exerce sobre o jato. Pela terceira lei de Newton, essa força que a placa exerce sobre o jato é igual em módulo à força de reação que o jato exerce sobre a placa. é o diâmetro do jato.
O volume de controle se movimenta junto com a placa. Por isso, a velocidade do volume de controle é igual à velocidade da placa .
Passo 2
Agora precisamos lembrar da fórmula de que encontramos no Problema 6-32. Ela se encontra abaixo.
é a densidade d aágua líquida a pressão atmosférica. Ela vale:
Além disso, para usar esa fórmula precisamos converter o diâmetro do jato de centímetro para metro .
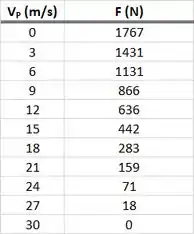
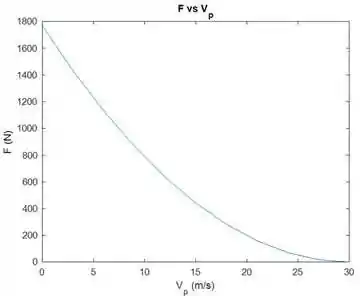
Agora vamos calcular o valor de para várias velocidades da placa. Seguem abaixo um vetorcom todas as velocidades que usaremos. Todas essas velocidades estão em .
Passo 3
Para calcular todos valores de rapidamente, podemos executar um algoritmo no MATLAB. O algoritmo que foi usado para gerar o gráfico e a tabela se encontra abaixo.

Passo 4
A tabela e o gráfico do resultado se encontram abaixo.
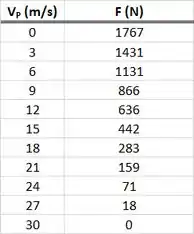
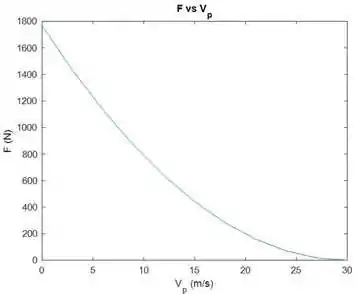
Resposta