Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 2.Problemas - Ex. 59
A tensão superficial de um líquido deve ser medida usando-se uma película líquida suspensa numa armação de arame em forma de U com um lado móvel de de comprimento. Se a força necessária para mover o arame for de , determine a tensão superficial desse líquido no ar.
Passo 1
O exercício quer saber quanto vale a tensão superficial de uma película de líquido que está sendo esticada. Os dados que o enunciado nos fornece são mostrados na figura abaixo.
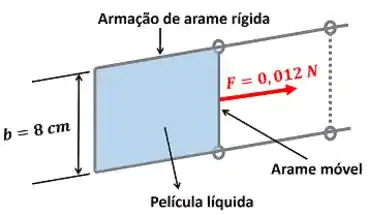
onde é a força com a qual a película está sendo esticada e é o tamanho do lado móvel.
No próximo passo, vamos aprender a calcular .
Passo 2
A equação do livro fornece uma fórmula para a gente calcular a tensão superficial .
Atenção! Antes de iniciar as contas, temos que converter de centímetro para metro .
Passo 3
Resposta
Exercícios de Livros Relacionados
Explique como um patim interage com a superfície de gelo. Que mecanismos agem no sentido de reduzir o atrito de deslizamento entre o patim e o gelo?
Um bloco cúbico de massa 10k g e de aresta de 250m m é puxado para cima em uma superfície inclinada, sobre o qual há um filme de óleo SAE 10W-30 a -1,1°C de espessura 0,025m m . Determine a velocidade
Uma patinadora de estilo livre no gelo desliza sobre patins à velocidade V = 6m / s . O seu peso, 450N , é suportado por uma fina película de água fundida do gelo pela pressão da lâmina do patim. Cons
A distribuição de velocidade para o escoamento laminar desenvolvido entre placas paralelas é dada por u u m á x = 1 - 2 y h 2 á Em que h é a distância separando as placas e a origem está situada na li
A distribuição de velocidade para o escoamento laminar desenvolvido entre placas paralelas é dada por u u m á x = 1 - 2 y h 2 á Em que h é a distância separando as placas; a origem está situada na lin