Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 4
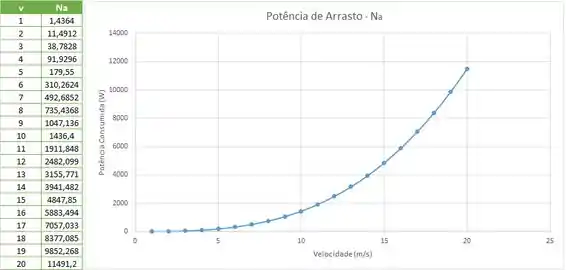
Os testes com um automóvel revelaram que ele tem um coeficiente de arrasto constante igual a . A área projetada é considerada . Construir um gráfico da potência necessária para vencer a resistência do ar em função da velocidade. (
Passo 1
A questão nos dá:
- O coeficiente de arrasto
- Área de referência:
- Densidade do ar:
A questão nos pede para desenhar um gráfico de potência necessária para vencer a resistência do ar.
Passo 2
Pela fórmula da potência temos:
Para a potência consumida pelo arrasto temos:
Onde é a força de arrasto e é a velocidade do ar. Substituíndo a fórmula da força de arrasto:
Organizando:
Substituindo os valores:
Chegamos na equação:
Onde a velocidade é dada em metros por segundo e a potência em watts.
Passo 3
Utilizando o Excel, podemos gerar um gráfico:
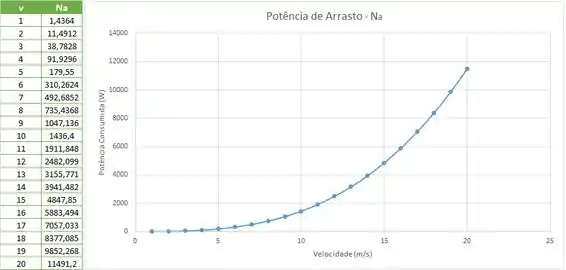
Resposta
Exercícios de Livros Relacionados
Uma barcaça de casco chato de 20 m de comprimento e 7 m de largura está imersa em profundidade de 1,5 m e deve ser empurrada com uma velocidade de 3,6 km/h. Estimar a potência necessária para efetuar
Uma esfera de 15 cm de diâmetro é colocada numa corrente de ar de ρ = 1,2 k g m 3 . O dinamômetro indica uma força de 1,14N . Qual é a velocidade do ar? ( ν a r = 10 - 5 m 2 s )
Água escoa sob uma placa plana de 10c m de comprimento e 20c m de largura, com uma velocidade de 0,1m / s . Determinar a força de arrasto que age na placa. ( ν = 10 - 6 m 2 / s e ρ = 1000k g / m 3
Uma gota de chuva tem diâmetro médio de 2,5m m . Calcular a velocidade limite da gota se o ar tem ρ = 1,2k g / m 3 e ν = 1,8 ⋅ 10 - 6 m 2 / s
Deseja-se impulsionar uma embarcação de 10 5 N de peso à velocidade de 72k m / h . A embarcação é sustentada por uma asa submarina cujos coeficientes de sustentação e arrasto são, respectivamente, 0,7