Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 9.Exercício - Ex. 7

Deseja-se impulsionar uma embarcação de 10 5 N de peso à velocidade de 72   k m / h . A embarcação é sustentada por uma asa submarina cujos coeficientes de sustentação e arrasto são, respectivamente, 0,7 e 0,06 . Determinar:

  1. Área da asa.
  2. A potência necessária para a propulsão.

Passo 1

Dados da questão:

  • Peso do barco: P = 10 5   N .
  • Velocidade: v = 72   k m / h = 20   m / s .
  • Coeficiente de sustentação: C s = 0,7 .
  • Coeficiente de arrasto: C a = 0,06 .
  • Densidade da água: ρ H 2 O = 1000   k g / m 3

A questão pede:

  • Área da asa
  • A potência necessária para propulsão

Passo 2

Vamos considerar que o arrasto e sustentação na asa são muito maiores do que em todo o resto, então podemos desconsiderar todas as outras regiões da embarcação.

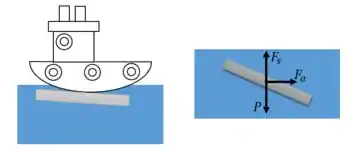
Para se manter flutuando, a força de sustentação tem que ser igual ao peso total da embarcação:

F s = P

Aplicando a equação da sustentação:

C s ⋅ ρ f l u i d o ⋅ v 2 2 A a s a = P

Isolando a área:

A a s a = P C s ⋅ ρ f l u i d o ⋅ v 2 2

Aplicando os valores:

A a s a = 2 ⋅ 10 5   N 0,7 ⋅ 1000 k g m 3 ⋅ 20 m s 2

A área da asa é:

A a s a = 0,714   m 3

Passo 3

A potência é o produto entre força e velocidade:

N = F a ⋅ v

Aplicando a equação do arrasto. Vamos considerar a área de referência iguais tanto para o arrasto quanto para a sustentação:

N = C a ⋅ ρ f l u i d o ⋅ v 2 2 A a s a ⋅ v

N = C a ⋅ ρ f l u i d o ⋅ v 3 2 A a s a

N = 0,06 ⋅ 1000 k g m 3 ⋅ 20 m s 3 2 ⋅ 0,714   m 2

N = 171360   W

Resposta

A a s a = 0,714   m 3

N = 171,36   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um anemômetro simples, porém eficaz, para medir a velocidade do vento, pode ser feito com uma placa fina pendurada de modo a defletir sob a ação do vento. Considere uma placa fina de latão, tendo 20 m
Uma grande roda de pás está imersa na correnteza de um rio para gerar potência. Cada pá tem área A e coeficiente de arrasto C A ; o centro de cada pá está localizado no raio R a partir da linha de cen
Considere a ciclista no Problema 9.99. Determine a máxima velocidade que ela pode realmente atingir hoje (com vento de 10 k m / h ), pedalando contra o vento e pedalando com o vento a favor. Se ela su
Um sistema de frenagem de emergência de um avião militar consiste em um grande paraquedas de 6 m de diâmetro. Se o avião tem massa de 8500 kg e aterrissa a 400 km/h, determine o tempo e a distância pa
Umdiscocircularépenduradoemumacorrentedearapartirdeumsuportearticulado,conformemostrado.Emumexperimento detúneldevento,realizadonoara15m/scomumdiscode25mmdediâmetro,∞foimedidocomo10°.Paraestascondiçõe