Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 35
Reconsidere o helicóptero do Problema 6-34, exceto que ele flutua no alto de uma montanha de de altitude na qual a densidade do ar é . Observando que as pás do helicóptero descarregado devem girar a para flutuar no nível do mar, determine a velocidade rotacional da pá para flutuar a uma altitude maior. Determine também o aumento percentual da entrada de potência necessária para flutuar a uma altitude de em relação àquela necessária para flutuar no nível do mar.
Passo 1
O enunciado quer saber primeiro a rotação em das pás do helicóptero quando ele está a uma altitude de . A figura abaixo mostra o volume de controle usado no Problema 6-34.
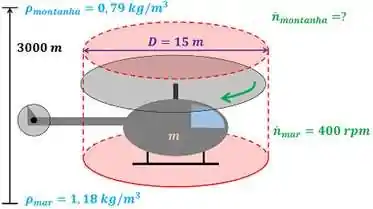
é a envergadura das pás do helicóptero. é a velocidade de rotação das pás do helicóptero em ao nível do mar. é a massa presente no volume de controle. Quando o helicópterio está sem carga, é apenas a massa do helicóptero. é a densidade do ar ao nível do mar. O enunciado do Problema 6-34 informa que vale:
é a densidade do ar ao nível da montanha.
Agora que lembramos um pouco da questão anterior, vamos aprender a calcular .
Passo 2
Podemos descobrir o valor de , lembrando que no enunciando do Problema 6-34 foi informado que a velocidade média do ar saindo do volume de controle é proporcional à velocidade rotacional da lâmina (rpm). Ou seja, é igual à multiplicação entre uma constante e .
A equação acima mostra que para encontrar , temos que achar . Achamos substituindo os valores de e para o caso no qual o helicóptero está ao nível do mar. Ressaltamos isso com um índice na velocidade e na velocidade de rotação .
A fórmula da velocidade no nível do mar é a fórmula encontrada na Problema 6-34.
Substituindo isso na fórmula, ela vira:
A velocidade do ar saindo do volume de controle a pode ser calculada com as mesmas fórmulas. A partir dessas fórmulas, somos capazes de criar uma fórmula para .
Substituindo uma fórmula na outra e cortando os termos iguais, achamos:
Passo 3
O enunciado também pede que a gente calcule o aumento percentual da potência , quando o helicóptero passa do nível do mar para de altura. A fórmula do aumento percentual é:
onde é a potência necessária para fazer o helicóptero ficar parado no ar ao nível do mar e é a potência necessária para fazer o helicóptero ficar parado no ar a de altura. e podem ser calculadas a partir da mesma fórmula deduzida no Problema 6-34. A única diferença entre os dois será na densidade do ar.
Substituindo isso na fórmula de , encontramos:
Passo 4
Substituindo os dados na equação de , encontramos seu valor.
Substituindo os dados na equação de , também encontramos seu valor.